In der Funktionentheorie , einem Teilgebiet der Mathematik , bilden die Jacobischen Thetafunktionen , benannt nach Carl Gustav Jakob Jacobi , eine spezielle Klasse holomorpher Funktionen zweier komplexer Variablen. Jacobi untersuchte sie als erster systematisch und entwickelte auf dieser Grundlage seine Theorie elliptischer Funktionen . Sie sind ein Spezialfall einer weitaus größeren Klasse von Thetafunktionen mehrerer Veränderlicher, die allgemein aus Gittern in den Räumen
R
n
{\displaystyle \mathbb {R} ^{n}}
Die Thetafunktionen bilden elliptische Gegenstücke der Exponentialfunktionen bzw. trigonometrischen Funktionen. Wie es für elliptische Funktionen typisch ist, weisen sie eine Art doppelter Periodizität auf entlang der reellen und der imaginären Richtung der komplexen Ebene (Gitterstruktur). Zugleich sind sie als unendliche Reihe sowie als unendliches Produkt darstellbar, deren Summanden beziehungsweise Faktoren in einer Vielzahl von Varianten aus Produkten von Exponential- und Cosinus- oder Sinusfaktoren bestehen.
Die Jacobischen Thetafunktionen spielen eine wichtige Rolle in der Theorie der elliptischen Funktionen, Modulformen , quadratischen Formen und der Modulräume . In der Physik sind sie zudem bei der Lösung der Diffusionsgleichung und bei der Lösung der Wärmeleitungsgleichung , dem sogenannten Wärmeleitungskern , von Bedeutung.
Eingeführt wurden die Thetafunktionen 1829 von Carl Gustav Jacobi, der diese Funktionen in seinem Buch Fundamenta nova theoriae functionum ellipticarum niederschrieb. Jacobi verwendete für diese Funktionengruppe den griechischen Buchstaben
Θ
{\displaystyle \Theta }
Thetafunktion . Sie ist bei Jacobi die Grundlage seiner Behandlung elliptischer Funktionen. Jacobi behandelte die Thetafunktionen, die elliptischen Amplitudenfunktionen und andere mehrfach periodische komplexe Funktionen in seinen Vorlesungen[ 1] Albertus-Universität Königsberg und entwickelte diese systematisch. Die Bedeutung der Thetafunktion für die Theorie elliptischer Funktionen erkannte schon Carl Friedrich Gauß insbesondere im Zusammenhang mit dem arithmetisch-geometrischen Mittel (AGM), er veröffentlichte aber nicht darüber. Die Thetafunktion selbst war in Spezialfällen schon Leonhard Euler und Johann I Bernoulli bekannt[ 2] Karl Weierstraß , Bernhard Riemann , Ferdinand Georg Frobenius und Henri Poincaré , der die Thetafunktionen in seinen Forschungen über die verallgemeinerten Eisenstein-Reihen analysierte.
Die klassische Jacobische Thetafunktion ist definiert durch:
ϑ
(
z
,
τ
)
:=
∑
n
=
−
∞
∞
e
π
i
n
2
τ
+
2
π
i
n
z
{\displaystyle \vartheta (z,\tau ):=\sum _{n=-\infty }^{\infty }e^{\pi in^{2}\tau +2\pi inz}}
Dabei ist
z
∈
C
{\displaystyle z\in \mathbb {C} }
τ
∈
H
{\displaystyle \tau \in \mathbb {H} }
oberen Halbebene
H
=
{
τ
∈
C
∣
ℑ
(
τ
)
>
0
}
{\displaystyle \mathbb {H} =\{\tau \in \mathbb {C} \mid \Im (\tau )>0\}}
Eulerschen Zahl und in Abhängigkeit vom Kreisbogenmaß
z
{\displaystyle z}
τ
{\displaystyle \tau }
n
{\displaystyle n}
C
×
H
{\displaystyle \mathbb {C} \times \mathbb {H} }
normal konvergent . Sie stellt eine in ganz
C
×
H
{\displaystyle \mathbb {C} \times \mathbb {H} }
τ
∈
H
{\displaystyle \tau \in \mathbb {H} }
z
↦
ϑ
(
z
,
τ
)
{\displaystyle z\mapsto \vartheta (z,\tau )}
ganze Funktion , und für festes
z
∈
C
{\displaystyle z\in \mathbb {C} }
τ
↦
ϑ
(
z
,
τ
)
{\displaystyle \tau \mapsto \vartheta (z,\tau )}
H
{\displaystyle \mathbb {H} }
holomorphe Funktion .
Funktion ϴ₁ mit Nomen 0,1·exp(0,1·i·π) Verallgemeinert wird die Thetafunktion so definiert:
Θ
a
,
b
(
z
,
τ
)
:=
∑
n
=
−
∞
∞
e
π
i
(
n
+
a
2
)
2
τ
+
2
π
i
(
n
+
a
2
)
z
+
π
i
n
b
{\displaystyle \Theta _{a,b}(z,\tau ):=\sum _{n=-\infty }^{\infty }e^{\pi i\left(n+{\frac {a}{2}}\right)^{2}\tau +2\pi i\left(n+{\frac {a}{2}}\right)z+\pi inb}}
Neben der klassischen Thetafunktion findet man in der Literatur vor allem drei weitere Thetafunktionen, die als Spezialfälle der klassischen Thetafunktion aufgestellt werden können. Diese drei weiteren Thetafunktionen entstehen, wenn die Parameter
a
{\displaystyle a}
b
{\displaystyle b}
Θ
0
(
z
,
τ
)
:=
Θ
0
,
1
(
z
,
τ
)
:=
ϑ
(
z
+
1
2
,
τ
)
=
∑
n
=
−
∞
∞
(
−
1
)
n
⋅
e
π
i
n
2
τ
+
2
π
i
n
z
{\displaystyle \Theta _{0}(z,\tau ):=\Theta _{0,1}(z,\tau ):=\vartheta \left(z+{\frac {1}{2}},\tau \right)=\sum _{n=-\infty }^{\infty }(-1)^{n}\cdot e^{\pi in^{2}\tau +2\pi inz}}
Θ
2
(
z
,
τ
)
:=
Θ
1
,
0
(
z
,
τ
)
:=
e
π
i
τ
4
+
π
i
z
⋅
ϑ
(
z
+
τ
2
,
τ
)
=
∑
n
=
−
∞
∞
e
π
i
(
n
+
1
2
)
2
τ
+
2
π
i
(
n
+
1
2
)
z
{\displaystyle \Theta _{2}(z,\tau ):=\Theta _{1,0}(z,\tau ):=e^{\pi i{\frac {\tau }{4}}+\pi iz}\cdot \vartheta \left(z+{\frac {\tau }{2}},\tau \right)=\sum _{n=-\infty }^{\infty }e^{\pi i\left(n+{\frac {1}{2}}\right)^{2}\tau +2\pi i\left(n+{\frac {1}{2}}\right)z}}
Θ
1
(
z
,
τ
)
:=
−
Θ
1
,
1
(
z
,
τ
)
:=
−
e
π
i
τ
4
+
π
i
(
z
+
1
2
)
⋅
ϑ
(
z
+
τ
+
1
2
,
τ
)
=
−
i
⋅
∑
n
=
−
∞
∞
(
−
1
)
n
⋅
e
π
i
(
n
+
1
2
)
2
τ
+
2
π
i
(
n
+
1
2
)
z
{\displaystyle \Theta _{1}(z,\tau ):=-\Theta _{1,1}(z,\tau ):=-e^{\pi i{\frac {\tau }{4}}+\pi i\left(z+{\frac {1}{2}}\right)}\cdot \vartheta \left(z+{\frac {\tau +1}{2}},\tau \right)=-i\cdot \sum _{n=-\infty }^{\infty }(-1)^{n}\cdot e^{\pi i\left(n+{\frac {1}{2}}\right)^{2}\tau +2\pi i\left(n+{\frac {1}{2}}\right)z}}
Die jacobische Thetafunktion wird in dieser Schreibweise als Θ₃(z,𝜏) bzw. Θ₀,₀(z,𝜏) bezeichnet.
Die Mathematiker Edmund Taylor Whittaker und George Neville Watson definierten folgende Thetafunktionen:[ 3] [ 4] [ 5]
ϑ
00
(
v
;
w
)
=
∏
n
=
1
∞
(
1
−
w
2
n
)
[
1
+
2
cos
(
2
v
)
w
2
n
−
1
+
w
4
n
−
2
]
{\displaystyle \vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]}
ϑ
01
(
v
;
w
)
=
∏
n
=
1
∞
(
1
−
w
2
n
)
[
1
−
2
cos
(
2
v
)
w
2
n
−
1
+
w
4
n
−
2
]
{\displaystyle \vartheta _{01}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n-1}+w^{4n-2}]}
ϑ
10
(
v
;
w
)
=
2
w
1
/
4
cos
(
v
)
∏
n
=
1
∞
(
1
−
w
2
n
)
[
1
+
2
cos
(
2
v
)
w
2
n
+
w
4
n
]
{\displaystyle \vartheta _{10}(v;w)=2w^{1/4}\cos(v)\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n}+w^{4n}]}
ϑ
11
(
v
;
w
)
=
−
2
w
1
/
4
sin
(
v
)
∏
n
=
1
∞
(
1
−
w
2
n
)
[
1
−
2
cos
(
2
v
)
w
2
n
+
w
4
n
]
{\displaystyle \vartheta _{11}(v;w)=-2w^{1/4}\sin(v)\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n}+w^{4n}]}
Das Theta-Symbol trägt bei diesen Definitionen unten rechts von sich zwei Indizes, die stets die Werte Null und Eins sind. Der linke Theta-Index bewirkt die Verschiebung des Exponentenindex
n
{\displaystyle n}
v
{\displaystyle v}
v
{\displaystyle v}
−
1
<
w
<
1
{\displaystyle -1<w<1}
elliptische Nomen in Abhängigkeit zum imaginären Halbperiodenverhältnis erfüllt die Gleichung
q
=
exp
(
i
π
τ
)
{\displaystyle q=\exp(i\pi \tau )}
Dabei gilt dieser Zusammenhang:
ϑ
00
[
π
z
;
exp
(
i
π
τ
)
]
=
Θ
0
,
0
(
z
,
τ
)
{\displaystyle \vartheta _{00}[\pi z;\exp(i\pi \tau )]=\Theta _{0,0}(z,\tau )}
ϑ
01
[
π
z
;
exp
(
i
π
τ
)
]
=
Θ
0
,
1
(
z
,
τ
)
{\displaystyle \vartheta _{01}[\pi z;\exp(i\pi \tau )]=\Theta _{0,1}(z,\tau )}
ϑ
10
[
π
z
;
exp
(
i
π
τ
)
]
=
Θ
1
,
0
(
z
,
τ
)
{\displaystyle \vartheta _{10}[\pi z;\exp(i\pi \tau )]=\Theta _{1,0}(z,\tau )}
Im Folgenden werden die Funktionen aus jeweils zwei Abszissen und einer Ordinate graphisch abgebildet:
Funktion - ϑ₁₁
Funktion ϑ₁₀
Funktion ϑ₀₀
Funktion ϑ₀₁
An diesen dreidimensionalen Graphenbildern ist die Tatsache erkennbar, dass die Funktionen ϑ₀₀ und ϑ₀₁ für Nomina 0 ≤ q < 1 stets positive Ordinatenwerte ergeben.
Unter dem Theta-Nullwert versteht man jeweils die Thetafunktion für den Wert
z
=
0
{\displaystyle z=0}
ϑ
(
τ
)
:=
ϑ
(
0
,
τ
)
=
∑
n
=
−
∞
∞
e
π
i
n
2
τ
=
1
+
2
∑
n
=
1
∞
e
π
i
n
2
τ
{\displaystyle \vartheta (\tau ):=\vartheta (0,\tau )=\sum _{n=-\infty }^{\infty }e^{\pi in^{2}\tau }=1+2\sum _{n=1}^{\infty }e^{\pi in^{2}\tau }}
Analog gilt mit der Definition nach Whittaker und Watson:
ϑ
00
(
0
;
x
)
=
ϑ
00
(
x
)
{\displaystyle \vartheta _{00}(0;x)=\vartheta _{00}(x)}
ϑ
01
(
0
;
x
)
=
ϑ
01
(
x
)
{\displaystyle \vartheta _{01}(0;x)=\vartheta _{01}(x)}
ϑ
10
(
0
;
x
)
=
ϑ
10
(
x
)
{\displaystyle \vartheta _{10}(0;x)=\vartheta _{10}(x)}
Durch Annullierung des Kreisbogenmaßes im linken Klammereintrag der allgemeinen Thetafunktion entstehen die drei sogenannten standardisierten Theta-Nullwertfunktionen. Bei diesen drei Funktionen hängt die Thetafunktion nur noch vom Nomen ab und somit zählen sie zu den Funktionen aus jeweils nur einer Variablen. Wenn der linke Klammereintrag auf Null gesetzt wird, so wird dieser bei den so entstehenden Theta-Nullwertfunktionen nicht mitgeschrieben und nur der rechte Klammereintrag wird als einziger Eintrag in der Klammer genannt. Durch Einsetzen des annullierten Bogenmaßwertes in die Summendefinition ergeben sich folgende drei Definitionsformeln[ 6]
ϑ
00
(
x
)
=
∑
k
=
−
∞
∞
x
k
2
=
∏
n
=
1
∞
(
1
−
x
2
n
)
(
1
+
x
2
n
−
1
)
2
{\displaystyle \vartheta _{00}(x)=\sum _{k=-\infty }^{\infty }x^{k^{2}}=\prod _{n=1}^{\infty }(1-x^{2n})(1+x^{2n-1})^{2}}
ϑ
01
(
x
)
=
∑
k
=
−
∞
∞
(
−
1
)
k
x
k
2
=
∏
n
=
1
∞
(
1
−
x
2
n
)
(
1
−
x
2
n
−
1
)
2
{\displaystyle \vartheta _{01}(x)=\sum _{k=-\infty }^{\infty }(-1)^{k}x^{k^{2}}=\prod _{n=1}^{\infty }(1-x^{2n})(1-x^{2n-1})^{2}}
ϑ
10
(
x
)
=
∑
k
=
−
∞
∞
x
(
k
+
1
2
)
2
=
2
x
1
/
4
∏
n
=
1
∞
(
1
−
x
2
n
)
(
1
+
x
2
n
)
2
{\displaystyle \vartheta _{10}(x)=\sum _{k=-\infty }^{\infty }x^{(k+{\frac {1}{2}})^{2}}=2x^{1/4}\prod _{n=1}^{\infty }(1-x^{2n})(1+x^{2n})^{2}}
Bei dieser Schreibweise gibt analog zu den obigen Formeln über die Produktreihendefinitionen die erste tiefgestellte Zahl nach dem Theta die Verschiebung der Exponentenbasis um 1/2 in der Summendarstellung an.
Die zweite tiefgestellte Zahl entscheidet über die Alternierung der Vorzeichen in der Summendarstellung. Im Werk Theta Functions and the Arithmetic-Geometric Mean Iteration von den Gebrüdern Borwein wurden die soeben gezeigten Summendefinitionen der drei grundlegenden Theta-Nullwertfunktionen auf der Seite 33 beschrieben. Außerdem gelten für die Quadrate der Thetafunktionen diese Beziehungen unter der Bedingung
|
x
|
<
1
{\displaystyle |x|<1}
ϑ
00
(
x
)
2
=
∑
n
=
−
∞
∞
2
x
n
1
+
x
2
n
{\displaystyle \vartheta _{00}(x)^{2}=\sum _{n=-\infty }^{\infty }{\frac {2x^{n}}{1+x^{2n}}}}
ϑ
01
(
x
)
2
=
∑
n
=
−
∞
∞
(
−
1
)
n
2
x
n
1
+
x
2
n
{\displaystyle \vartheta _{01}(x)^{2}=\sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}2x^{n}}{1+x^{2n}}}}
ϑ
10
(
x
)
2
=
∑
n
=
−
∞
∞
2
x
n
+
1
/
2
1
+
x
2
n
+
1
{\displaystyle \vartheta _{10}(x)^{2}=\sum _{n=-\infty }^{\infty }{\frac {2x^{n+1/2}}{1+x^{2n+1}}}}
Für festes
τ
∈
H
{\displaystyle \tau \in \mathbb {H} }
ϑ
(
z
,
τ
)
{\displaystyle \vartheta (z,\tau )}
z
=
k
+
m
τ
+
τ
+
1
2
,
k
,
m
∈
Z
{\displaystyle z=k+m\tau +{\frac {\tau +1}{2}},k,m\in \mathbb {Z} }
Die Thetafunktion ist periodisch in beiden Variablen, es gilt:
ϑ
(
z
+
1
,
τ
)
=
ϑ
(
z
,
τ
+
2
)
=
ϑ
(
z
,
τ
)
.
{\displaystyle \vartheta (z+1,\tau )=\vartheta (z,\tau +2)=\vartheta (z,\tau ).}
Dies ist eine Folgerung aus der 1-Periodizität der komplexen Exponentialfunktion
z
↦
e
2
π
i
z
{\displaystyle z\mapsto e^{2\pi iz}}
ϑ
(
z
,
−
1
τ
)
=
e
π
i
z
2
τ
τ
i
ϑ
(
z
τ
,
τ
)
.
{\displaystyle \vartheta \left(z,-{\frac {1}{\tau }}\right)=e^{\pi iz^{2}\tau }{\sqrt {\frac {\tau }{i}}}\vartheta (z\tau ,\tau ).}
Diese lässt erkennen, dass die Variable
τ
{\displaystyle \tau }
modular ist, da sie neben der 2-Periodizität noch ein Gesetz unter der Stürzung
τ
↦
−
1
τ
{\displaystyle \tau \mapsto -{\tfrac {1}{\tau }}}
ϑ
(
−
1
τ
)
=
τ
i
ϑ
(
τ
)
.
{\displaystyle \vartheta \left(-{\frac {1}{\tau }}\right)={\sqrt {\frac {\tau }{i}}}\vartheta (\tau ).}
Bei der Wurzel ist dabei jeweils der Hauptzweig zu nehmen, also jener Zweig, der positive Zahlen auf positive Zahlen abbildet.
Das Transformationsgesetz[ 7] poissonschen Summationsformel . Diese erlaubt es, die Fourier-Reihe von 1-periodischen Reihen des Typs
∑
n
=
−
∞
∞
f
(
n
+
x
)
{\displaystyle \sum _{n=-\infty }^{\infty }f(n+x)}
anzugeben. Ist
f
:
R
→
C
{\displaystyle f\colon \mathbb {R} \to \mathbb {C} }
glatte Funktion , deren sämtliche Ableitungen für
x
→
±
∞
{\displaystyle x\to \pm \infty }
g
:
R
→
C
{\displaystyle g\colon \mathbb {R} \to \mathbb {C} }
g
{\displaystyle g}
g
(
x
)
=
∑
n
=
−
∞
∞
f
(
n
+
x
)
=
∑
n
=
−
∞
∞
f
^
(
n
)
e
2
π
i
n
x
,
{\displaystyle g(x)=\sum _{n=-\infty }^{\infty }f(n+x)=\sum _{n=-\infty }^{\infty }{\hat {f}}(n)e^{2\pi inx},}
wobei
f
^
(
x
)
:=
∫
−
∞
∞
f
(
y
)
e
−
2
π
i
x
y
d
y
{\displaystyle {\hat {f}}(x):=\int _{-\infty }^{\infty }f(y)e^{-2\pi ixy}\mathrm {d} y}
die Fourier-Transformation von
f
{\displaystyle f}
f
{\displaystyle f}
f
^
{\displaystyle {\hat {f}}}
f
{\displaystyle f}
f
(
x
)
:=
e
−
π
x
2
{\displaystyle f(x):=e^{-\pi x^{2}}}
h
^
(
x
)
=
δ
−
1
f
^
(
δ
−
1
x
)
{\displaystyle {\hat {h}}(x)=\delta ^{-1}{\hat {f}}(\delta ^{-1}x)}
δ
>
0
{\displaystyle \delta >0}
h
(
x
)
:=
f
(
δ
x
)
{\displaystyle h(x):=f(\delta x)}
Substitution ergibt, findet man damit via
δ
:=
t
{\displaystyle \delta :={\sqrt {t}}}
t
:=
τ
i
{\displaystyle t:={\frac {\tau }{i}}}
τ
{\displaystyle \tau }
τ
i
e
π
i
z
2
τ
ϑ
(
z
τ
,
τ
)
=
t
e
−
π
z
2
t
ϑ
(
z
i
t
,
i
t
)
=
t
∑
n
=
−
∞
∞
e
−
π
(
n
+
z
)
2
t
=
∑
n
=
−
∞
∞
e
−
π
n
2
t
+
2
π
i
n
z
=
ϑ
(
z
,
i
t
)
=
ϑ
(
z
,
−
1
τ
)
.
{\displaystyle {\sqrt {\frac {\tau }{i}}}e^{\pi iz^{2}\tau }\vartheta (z\tau ,\tau )={\sqrt {t}}e^{-\pi z^{2}t}\vartheta (zit,it)={\sqrt {t}}\sum _{n=-\infty }^{\infty }e^{-\pi (n+z)^{2}t}=\sum _{n=-\infty }^{\infty }e^{-{\frac {\pi n^{2}}{t}}+2\pi inz}=\vartheta \left(z,{\frac {i}{t}}\right)=\vartheta \left(z,-{\frac {1}{\tau }}\right).}
Mittels des Identitätssatzes für holomorphe Funktionen dehnt sich diese Funktionalgleichung, wegen holomorpher Funktionen auf beiden Seiten, auf ganz
C
×
H
{\displaystyle \mathbb {C} \times \mathbb {H} }
Die Poissonsche Summenformel wird vor allem zu Fourier-analytischen Untersuchungen verwendet. Neben Siméon Poisson erforschten insbesondere Bernhard Riemann und der US-amerikanische Mathematiker Harold Mortimer Edwards Junior diese Thetafunktionsformel.
Die Thetafunktion lässt sich mit Hilfe des jacobischen Tripelproduktes auch als unendliches Produkt darstellen, es gilt:
ϑ
(
z
,
τ
)
=
∏
n
=
1
∞
(
1
−
e
2
π
i
n
τ
)
(
1
+
e
π
i
[
(
2
n
−
1
)
τ
+
2
z
]
)
(
1
+
e
π
i
[
(
2
n
−
1
)
τ
−
2
z
]
)
{\displaystyle \vartheta (z,\tau )=\prod _{n=1}^{\infty }(1-e^{2\pi in\tau })(1+e^{\pi i[(2n-1)\tau +2z]})(1+e^{\pi i[(2n-1)\tau -2z]})}
Speziell für den Theta-Nullwert reduziert sich dies auf
ϑ
(
τ
)
=
∏
n
=
1
∞
(
1
−
e
2
π
i
n
τ
)
(
1
+
e
π
i
(
2
n
−
1
)
τ
)
2
{\displaystyle \vartheta (\tau )=\prod _{n=1}^{\infty }(1-e^{2\pi in\tau })(1+e^{\pi i(2n-1)\tau })^{2}}
Aus dieser Darstellung folgt insbesondere, dass
ϑ
(
τ
)
{\displaystyle \vartheta (\tau )}
H
{\displaystyle \mathbb {H} }
Die Thetafunktion besitzt eine Integraldarstellung:
ϑ
(
z
,
τ
)
=
i
∫
i
−
∞
i
+
∞
e
i
π
τ
u
2
cos
(
2
π
u
z
+
π
u
)
sin
(
π
u
)
d
u
{\displaystyle \vartheta (z,\tau )=i\int _{i-\infty }^{i+\infty }{e^{i\pi \tau u^{2}}\cos(2\pi uz+\pi u) \over \sin(\pi u)}{\text{d}}u}
Die zugehörige Theta-Nullwertfunktion hat für positive x-Werte diese Integraldarstellung:
ϑ
00
(
x
)
=
1
+
4
x
π
∫
0
∞
exp
(
−
y
2
)
{
1
−
x
2
cos
[
2
ln
(
1
/
x
)
y
]
}
1
−
2
x
2
cos
[
2
ln
(
1
/
x
)
y
]
+
x
4
d
y
{\displaystyle \vartheta _{00}(x)=1+{\frac {4x}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp(-y^{2})\{1-x^{2}\cos[2{\sqrt {\ln(1/x)}}\,y]\}}{1-2x^{2}\cos[2{\sqrt {\ln(1/x)}}\,y]+x^{4}}}\,\mathrm {d} y}
Diese Formel wurde im Aufsatz Square series generating function transformations von der Mathematikerin Maxie Schmidt aus Georgia behandelt.
Die Theta-Nullwerte erfüllen die sogenannte Jacobi-Identität:
Θ
3
(
τ
)
4
=
Θ
0
(
τ
)
4
+
Θ
2
(
τ
)
4
{\displaystyle \Theta _{3}(\tau )^{4}=\Theta _{0}(\tau )^{4}+\Theta _{2}(\tau )^{4}}
Für die analogen Klein-Thetafunktionen gilt dieselbe Identität:
ϑ
00
(
x
)
4
=
ϑ
01
(
x
)
4
+
ϑ
10
(
x
)
4
{\displaystyle \vartheta _{00}(x)^{4}=\vartheta _{01}(x)^{4}+\vartheta _{10}(x)^{4}}
Verallgemeinert[ 8]
ϑ
00
(
a
+
b
;
c
)
ϑ
00
(
a
−
b
;
c
)
ϑ
00
(
c
)
2
=
ϑ
01
(
a
;
c
)
2
ϑ
01
(
b
;
c
)
2
+
ϑ
10
(
a
;
c
)
2
ϑ
10
(
b
;
c
)
2
{\displaystyle \vartheta _{00}(a+b;c)\vartheta _{00}(a-b;c)\vartheta _{00}(c)^{2}=\vartheta _{01}(a;c)^{2}\vartheta _{01}(b;c)^{2}+\vartheta _{10}(a;c)^{2}\vartheta _{10}(b;c)^{2}}
ϑ
01
(
a
+
b
;
c
)
ϑ
01
(
a
−
b
;
c
)
ϑ
01
(
c
)
2
=
ϑ
00
(
a
;
c
)
2
ϑ
00
(
b
;
c
)
2
−
ϑ
10
(
a
;
c
)
2
ϑ
10
(
b
;
c
)
2
{\displaystyle \vartheta _{01}(a+b;c)\vartheta _{01}(a-b;c)\vartheta _{01}(c)^{2}=\vartheta _{00}(a;c)^{2}\vartheta _{00}(b;c)^{2}-\vartheta _{10}(a;c)^{2}\vartheta _{10}(b;c)^{2}}
Diese Identitäten wurden insbesondere durch Whittaker und Watson erforscht. Exemplarische Abwandlungen dieser beiden Formeln wurden von den Autoren Irene Stegun und Milton Abramowitz in ihr weltbekanntes Handbuch der mathematischen Funktionen eingetragen.
Graph des Sekans hyperbolicus Gaußsche Glockenkurvenfunktion exp(-x²) mit Stammfunktion Im folgenden wird ein wichtiger Grenzwert der Funktion behandelt:
Für alle Werte y des Definitionsbereichs gilt:
Und für Werte |y| < 1 gilt:
∑
k
=
−
∞
∞
y
k
2
=
ϑ
00
(
y
)
{\displaystyle \sum _{k=-\infty }^{\infty }y^{k^{2}}=\vartheta _{00}(y)}
∑
k
=
−
∞
∞
2
y
k
y
2
k
+
1
=
ϑ
00
(
y
)
2
{\displaystyle \sum _{k=-\infty }^{\infty }{\frac {2y^{k}}{y^{2k}+1}}=\vartheta _{00}(y)^{2}}
Und es gilt für den Sekans hyperbolicus :
sech
(
x
)
=
2
exp
(
x
)
exp
(
2
x
)
+
1
{\displaystyle \operatorname {sech} (x)={\frac {2\exp(x)}{\exp(2x)+1}}}
Daraus resultiert diese Formel:
lim
n
→
∞
1
n
ϑ
00
[
exp
(
−
1
n
)
]
2
=
lim
n
→
∞
1
n
∑
k
=
−
∞
∞
sech
(
k
n
)
=
∫
−
∞
∞
sech
(
x
)
d
x
=
π
{\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n}}\right)\right]^{2}=\lim _{n\rightarrow \infty }{\frac {1}{n}}\sum _{k=-\infty }^{\infty }\operatorname {sech} \left({\frac {k}{n}}\right)=\int _{-\infty }^{\infty }\operatorname {sech} (x)\,\mathrm {d} x=\pi }
Die Definition des Riemannschen Integrals beschreibt die Umwandlung zwischen Grenzwert und Integral.
Danach kann jene Umformung durchgeführt werden:
Die Substitution
n
→
n
2
{\displaystyle n\rightarrow n^{2}}
Die quadratische Radizierung ergibt:
lim
n
→
∞
1
n
2
ϑ
00
[
exp
(
−
1
n
2
)
]
2
=
π
{\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n^{\color {ForestGreen}2}}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{\color {ForestGreen}2}}}\right)\right]^{2}=\pi }
lim
n
→
∞
1
n
ϑ
00
[
exp
(
−
1
n
2
)
]
=
π
{\displaystyle {\color {Navy}\lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{2}}}\right)\right]}={\sqrt {\pi }}}
Außerdem[ 9]
lim
n
→
∞
1
n
ϑ
00
[
exp
(
−
1
n
2
)
]
=
lim
n
→
∞
1
n
∑
k
=
−
∞
∞
exp
[
−
(
k
n
)
2
]
=
∫
−
∞
∞
exp
(
−
x
2
)
d
x
{\displaystyle {\color {Navy}\lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{2}}}\right)\right]}=\lim _{n\rightarrow \infty }{\frac {1}{n}}\sum _{k=-\infty }^{\infty }\exp \left[-\left({\frac {k}{n}}\right)^{2}\right]=\int _{-\infty }^{\infty }\exp(-x^{2})\,\mathrm {d} x}
Daraus folgt über die Gaußsche Glockenkurve dieses Resultat:
∫
−
∞
∞
exp
(
−
x
2
)
d
x
=
π
{\displaystyle \int _{-\infty }^{\infty }\exp(-x^{2})\,\mathrm {d} x={\sqrt {\pi }}}
Die grundlegenden modulären Identitäten der Theta-Nullwertfunktionen in Abhängigkeit von der Funktion des elliptischen Nomens [ 10] Jacobischen Entwicklungsgröße lauten so:
ϑ
00
[
q
(
k
)
]
=
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[q(k)]={\sqrt {2\pi ^{-1}K(k)}}}
ϑ
01
[
q
(
k
)
]
=
1
−
k
2
4
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{01}[q(k)]={\sqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
10
[
q
(
k
)
]
=
|
k
|
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{10}[q(k)]={\sqrt {|k|}}\,{\sqrt {2\pi ^{-1}K(k)}}}
An der Gegenüberstellung dieser drei Formeln ist die Jacobische Identität erkennbar. Der Kleinbuchstabe q steht für das elliptische Nomen und diese Funktion wird so definiert:
q
(
k
)
=
exp
[
−
π
K
(
1
−
k
2
)
K
(
k
)
]
{\displaystyle q(k)=\exp {\biggl [}-\pi \,{\frac {K({\sqrt {1-k^{2}}})}{K(k)}}{\biggr ]}}
Der in der Exponentialfunktionsklammer der Definition des elliptischen Nomens gezeigte Quotient aus dem K -Integral des pythagoräisch komplementären Moduls dividiert durch das K -Integral des Moduls selbst wird als reelles Viertelperiodenverhältnis oder auch als reelles Halbperiodenverhältnis bezeichnet. Der Großbuchstabe K selbst bringt das vollständige elliptische Integral erster Art beziehungsweise die jacobische Viertelperiode zum Ausdruck. Das vollständige elliptische Integral erster Art ist eine Funktion in Abhängigkeit von exakt einer Variable. Und diese Variable wird elliptischer Modul oder auch numerische Exzentrizität genannt. Das mit dem großen K bezeichnete vollständige elliptische Integral erster Art kann nach Adrien Marie Legendre mit folgender Summe und mit folgenden Integralen in Abhängigkeit vom Modul ε oder k definiert werden:
K
(
ε
)
=
π
2
∑
n
=
0
∞
[
(
2
n
)
!
]
2
16
n
(
n
!
)
4
ε
2
n
{\displaystyle K(\varepsilon )={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}\,\varepsilon ^{2n}}
K
(
ε
)
=
∫
0
π
/
2
1
1
−
ε
2
sin
(
φ
)
2
d
φ
=
∫
0
1
1
(
1
−
x
2
)
(
1
−
ε
2
x
2
)
d
x
{\displaystyle K(\varepsilon )=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-\varepsilon ^{2}\sin(\varphi )^{2}}}}\,\mathrm {d} \varphi =\int _{0}^{1}{\frac {1}{\sqrt {(1-x^{2})(1-\varepsilon ^{2}x^{2})}}}\,\mathrm {d} x}
Die Thetafunktion hängt eng zusammen mit der Dedekindschen Etafunktion , es gilt:
ϑ
(
0
,
τ
)
=
η
2
(
τ
+
1
2
)
η
(
τ
+
1
)
{\displaystyle \vartheta (0,\tau )={\frac {\eta ^{2}({\frac {\tau +1}{2}})}{\eta (\tau +1)}}}
Mittels der Thetafunktion lassen sich Modulformen definieren. Setzt man
f
(
τ
)
:=
ϑ
8
(
τ
)
{\displaystyle f(\tau ):=\vartheta ^{8}(\tau )}
f
(
τ
+
2
)
=
f
(
τ
)
und
f
(
−
1
τ
)
=
τ
4
f
(
τ
)
{\displaystyle f(\tau +2)=f(\tau )\quad {\text{und}}\quad f\left(-{\frac {1}{\tau }}\right)=\tau ^{4}f(\tau )}
Die Funktion
f
(
τ
)
{\displaystyle f(\tau )}
Modulform vom Gewicht 4 zu der von den beiden Transformationen
τ
↦
τ
+
2
{\displaystyle \tau \mapsto \tau +2}
τ
↦
−
1
τ
{\displaystyle \tau \mapsto -{\tfrac {1}{\tau }}}
Untergruppe
Γ
ϑ
{\displaystyle \Gamma _{\vartheta }}
Modulgruppe
Γ
{\displaystyle \Gamma }
Die Thetafunktion lässt sich zur Definition elliptischer Funktionen heranziehen. Setzt man etwa für festes
τ
∈
H
:
{\displaystyle \tau \in \mathbb {H} \colon }
f
(
z
)
=
ϑ
2
(
z
+
1
2
,
τ
)
ϑ
2
(
z
,
τ
)
{\displaystyle f(z)={\frac {\vartheta ^{2}(z+{\frac {1}{2}},\tau )}{\vartheta ^{2}(z,\tau )}}}
so ist
f
(
z
)
{\displaystyle f(z)}
Gitter
Z
+
Z
τ
{\displaystyle \mathbb {Z} +\mathbb {Z} \tau }
Auf ähnliche Weise lässt sich auch die Weierstraßsche ℘-Funktion konstruieren. Erfüllt nämlich eine holomorphe Funktion
f
(
z
)
{\displaystyle f(z)}
f
(
z
+
1
)
=
f
(
z
)
{\displaystyle f(z+1)=f(z)}
f
(
z
+
τ
)
=
e
−
a
z
−
b
f
(
z
)
{\displaystyle f(z+\tau )={\text{e}}^{-az-b}f(z)}
für ein festes
τ
∈
H
{\displaystyle \tau \in \mathbb {H} }
logarithmische Ableitung eine elliptische Funktion zum Gitter
Z
+
Z
τ
{\displaystyle \mathbb {Z} +\mathbb {Z} \tau }
℘
(
z
)
=
−
d
2
d
z
2
log
Θ
1
(
z
,
τ
)
+
c
{\displaystyle \wp (z)=-{\frac {{\text{d}}^{2}}{{\text{d}}z^{2}}}\log \Theta _{1}(z,\tau )+c}
mit einer passenden Konstanten
c
{\displaystyle c}
Die Maclaurinsche Reihe [ 11] ϑ₀₁ hat als Koeffizienten die Zahlen der Oberpartitionsfolge mit stets positivem Vorzeichen:
1
ϑ
01
(
x
)
=
∏
n
=
1
∞
1
+
x
n
1
−
x
n
=
∑
k
=
0
∞
P
¯
(
k
)
x
k
{\displaystyle {\frac {1}{\vartheta _{01}(x)}}=\prod _{n=1}^{\infty }{\frac {1+x^{n}}{1-x^{n}}}=\sum _{k=0}^{\infty }{\overline {P}}(k)x^{k}}
1
ϑ
01
(
x
)
=
1
+
2
x
+
4
x
2
+
8
x
3
+
14
x
4
+
24
x
5
+
40
x
6
+
64
x
7
+
100
x
8
+
154
x
9
+
232
x
10
+
…
{\displaystyle {\frac {1}{\vartheta _{01}(x)}}=1+2x+4x^{2}+8x^{3}+14x^{4}+24x^{5}+40x^{6}+64x^{7}+100x^{8}+154x^{9}+232x^{10}+\dots }
Wenn zu einer gegebenen Zahl
k
{\displaystyle k}
[ 12]
k
{\displaystyle k}
P
¯
(
k
)
{\displaystyle {\overline {P}}(k)}
Erstes Beispiel:
P
¯
(
4
)
=
14
{\displaystyle {\overline {P}}(4)=14}
Diese 14 Möglichkeiten der Partitionsmarkierungen existieren für die Summe 4:
(4), (4 ), (3+1), (3 +1), (3+1 ), (3 +1 ), (2+2), (2 +2), (2+1+1), (2 +1+1), (2+1 +1), (2 +1 +1), (1+1+1+1), (1 +1+1+1)
Zweites Beispiel:
P
¯
(
5
)
=
24
{\displaystyle {\overline {P}}(5)=24}
Diese 24 Möglichkeiten der Partitionsmarkierungen existieren für die Summe 5:
(5), (5 ), (4+1), (4 +1), (4+1 ), (4 +1 ), (3+2), (3 +2), (3+2 ), (3 +2 ), (3+1+1), (3 +1+1), (3+1 +1), (3 +1 +1), (2+2+1), (2 +2+1), (2+2+1 ), (2 +2+1 ),
(2+1+1+1), (2 +1+1+1), (2+1 +1+1), (2 +1 +1+1), (1+1+1+1+1), (1 +1+1+1+1)
Halblogarithmische Darstellung der Partitionsfunktion
P
(
n
)
{\displaystyle P(n)}
Die reguläre Partitionsfolge
P
(
n
)
{\displaystyle P(n)}
ganze Zahl
n
{\displaystyle n}
Summanden zerlegt werden kann. Für die Zahlen
n
=
1
{\displaystyle n=1}
n
=
5
{\displaystyle n=5}
P
{\displaystyle P}
Beispielwerte von P(n) und zugehörige Zahlpartitionen
n
P(n)
Zahlpartitionen
0
1
() leere Partition/leere Summe
1
1
(1)
2
2
(1+1), (2)
3
3
(1+1+1), (1+2), (3)
4
5
(1+1+1+1), (1+1+2), (2+2), (1+3), (4)
5
7
(1+1+1+1+1), (1+1+1+2), (1+2+2), (1+1+3), (2+3), (1+4), (5)
Die erzeugende Funktion der regulären Partitionszahlenfolge kann auf folgende Weise über das Pochhammersche Produkt dargestellt werden:
∑
k
=
0
∞
P
(
k
)
x
k
=
1
(
x
;
x
)
∞
{\displaystyle \sum _{k=0}^{\infty }P(k)x^{k}={\frac {1}{(x;x)_{\infty }}}}
Und die strikte Partitionsfolge
Q
(
n
)
{\displaystyle Q(n)}
n
{\displaystyle n}
[ 13] [ 14] [ 15]
Beispielwerte von Q(n) und zugehörige Zahlpartitionen
n
Q(n)
Zahlpartitionen ohne wiederholte Summanden
Zahlpartitionen mit nur ungeraden Summanden
0
1
() leere Partition/leere Summe
() leere Partition/leere Summe
1
1
(1)
(1)
2
1
(2)
(1+1)
3
2
(1+2), (3)
(1+1+1), (3)
4
2
(1+3), (4)
(1+1+1+1), (1+3)
5
3
(2+3), (1+4), (5)
(1+1+1+1+1), (1+1+3), (5)
6
4
(1+2+3), (2+4), (1+5), (6)
(1+1+1+1+1+1), (1+1+1+3), (3+3), (1+5)
7
5
(1+2+4), (3+4), (2+5), (1+6), (7)
(1+1+1+1+1+1+1), (1+1+1+1+3), (1+3+3), (1+1+5), (7)
8
6
(1+3+4), (1+2+5), (3+5), (2+6), (1+7), (8)
(1+1+1+1+1+1+1+1), (1+1+1+1+1+3), (1+1+3+3), (1+1+1+5), (3+5), (1+7)
Die erzeugende Funktion der strikten Partitionszahlenfolge kann so über das Pochhammersche Produkt dargestellt werden:
∑
k
=
0
∞
Q
(
k
)
x
k
=
1
(
x
;
x
2
)
∞
{\displaystyle \sum _{k=0}^{\infty }Q(k)x^{k}={\frac {1}{(x;x^{2})_{\infty }}}}
In der Online-Enzyklopädie der Zahlenfolgen beziehungsweise Online Encyclopedia of Integer Sequences (OEIS) ist die Folge der regulären Partitionszahlen
P
(
n
)
{\displaystyle P(n)}
Q
(
n
)
{\displaystyle Q(n)}
P
¯
(
n
)
{\displaystyle {\overline {P}}(n)}
n
=
1
{\displaystyle n=1}
Die Folge der Oberpartitionen
P
¯
(
n
)
{\displaystyle {\overline {P}}(n)}
[ 16] [ 17]
P
¯
(
n
)
=
∑
k
=
0
n
P
(
n
−
k
)
Q
(
k
)
{\displaystyle {\overline {P}}(n)=\sum _{k=0}^{n}P(n-k)Q(k)}
In der folgenden Tabelle der Zahlenfolgen soll diese nun gezeigte Formel exemplarisch angewendet werden:
n
P(n)
Q(n)
P
¯
(
n
)
{\displaystyle {\overline {P}}(n)}
0
1
1
1 = 1·1
1
1
1
2 = 1·1 + 1·1
2
2
1
4 = 2·1 + 1·1 + 1·1
3
3
2
8 = 3·1 + 2·1 + 1·1 + 1·2
4
5
2
14 = 5·1 + 3·1 + 2·1 + 1·2 + 1·2
5
7
3
24 = 7·1 + 5·1 + 3·1 + 2·2 + 1·2 + 1·3
Mit dieser Eigenschaft zusammenhängend kann über die Funktion ϑ₀₁ auch folgende Kombination zweier Summenreihen aufgestellt werden:
ϑ
01
(
x
)
=
[
∑
k
=
0
∞
P
(
k
)
x
k
]
−
1
[
∑
k
=
0
∞
Q
(
k
)
x
k
]
−
1
{\displaystyle \vartheta _{01}(x)={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}{\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}}
Srinivasa Ramanujan (श्रीनिवास रामानुजन) Julius Wilhelm Richard Dedekind Das Nomen-Pochhammer-Symbol ist so definiert:
(
y
;
z
)
∞
=
∏
k
=
0
∞
(
1
−
y
z
k
)
{\displaystyle (y;z)_{\infty }=\prod _{k=0}^{\infty }(1-yz^{k})}
Für folgendes unendliche Produkt in Darstellung mit dem Pochhammer-Symbol gilt diese Identität:
(
x
;
x
2
)
∞
=
[
∑
k
=
0
∞
Q
(
k
)
x
k
]
−
1
=
ϑ
00
(
x
)
−
1
/
6
ϑ
01
(
x
)
1
/
3
[
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
16
x
]
−
1
/
24
{\displaystyle (x;x^{2})_{\infty }={\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}=\vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}}
Dieses Produkt ist zugleich der Kehrwert von der erzeugenden Funktion der strikten Partitionszahlenfolge Q(n) und hat die genannte Identität zu den Theta-Nullwertfunktionen. Srinivasa Ramanujan entdeckte diese Identität zu den Thetafunktionen und schrieb sie in seinem berühmten Werk Modular Equations and Approximations to π nieder.[ 18] Richard Dedekind erkannt[ 19] Etafunktion behandelt. Eng verwandt mit dem genannten Produkt ist das Eulersche Pochhammer-Produkt, das der Kehrwert der erzeugenden Funktion von der regulären Partitionszahlenfolge P(n) ist. Für das Eulersche Produkt gilt folgende Identität:[ 20] [ 19]
(
x
;
x
)
∞
=
[
∑
k
=
0
∞
P
(
k
)
x
k
]
−
1
=
ϑ
00
(
x
)
1
/
6
ϑ
01
(
x
)
2
/
3
[
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
16
x
]
1
/
24
{\displaystyle (x;x)_{\infty }={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}=\vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}}
Es gilt für die beiden zuletzt genannten Formeln der Gültigkeitsbereich
−
1
<
x
<
1
{\displaystyle -1<x<1}
x
{\displaystyle x}
Das Produkt aus diesen beiden Pochhammer-Produkten liefert direkt das Resultat einer Definition:
(
x
;
x
)
∞
(
x
;
x
2
)
∞
=
ϑ
01
(
x
)
{\displaystyle (x;x)_{\infty }(x;x^{2})_{\infty }=\vartheta _{01}(x)}
Mit Hilfe der Thetafunktion und deren Produktdarstellung lässt sich der Pentagonalzahlensatz beweisen. Der Pentagonalzahlensatz hat diese definierende[ 21]
(
x
;
x
)
∞
=
1
+
∑
n
=
1
∞
[
−
x
Fn
(
2
n
−
1
)
−
x
Kr
(
2
n
−
1
)
+
x
Fn
(
2
n
)
+
x
Kr
(
2
n
)
]
{\displaystyle (x;x)_{\infty }=1+\sum _{n=1}^{\infty }{\bigl [}-x^{{\text{Fn}}(2n-1)}-x^{{\text{Kr}}(2n-1)}+x^{{\text{Fn}}(2n)}+x^{{\text{Kr}}(2n)}{\bigr ]}}
Hierbei gelten für die Fünfeckszahlen und die Kartenhauszahlen diese grundlegenden Definitionen:
Fn
(
z
)
=
1
2
z
(
3
z
−
1
)
{\displaystyle {\text{Fn}}(z)={\tfrac {1}{2}}z(3z-1)}
Kr
(
z
)
=
1
2
z
(
3
z
+
1
)
{\displaystyle {\text{Kr}}(z)={\tfrac {1}{2}}z(3z+1)}
Als weitere Anwendung[ 22]
(
x
;
x
)
3
=
∏
n
=
1
∞
(
1
−
x
n
)
3
=
∑
m
=
0
∞
(
−
1
)
m
(
2
m
+
1
)
x
m
(
m
+
1
)
/
2
{\displaystyle (x;x)^{3}=\prod _{n=1}^{\infty }(1-x^{n})^{3}=\sum _{m=0}^{\infty }(-1)^{m}(2m+1)x^{m(m+1)/2}}
Im Folgenden sollen exemplarisch drei wichtige Thetafunktionswerte hergeleitet werden:
So ist die Eulersche Betafunktion in ihrer reduzierten Form definiert:
β
(
x
)
=
Γ
(
x
)
2
Γ
(
2
x
)
{\displaystyle \beta (x)={\frac {\Gamma (x)^{2}}{\Gamma (2x)}}}
Generell ist für allen natürlichen Zahlen n ∈ ℕ diese Formel über die Eulersche Betafunktion gültig:
4
−
1
/
(
n
+
2
)
n
+
2
csc
(
π
n
+
2
)
β
[
n
2
(
n
+
2
)
]
=
∫
0
∞
1
x
n
+
2
+
1
d
x
{\displaystyle {\frac {4^{-1/(n+2)}}{n+2}}\csc {\bigl (}{\frac {\pi }{n+2}}{\bigr )}\beta {\biggl [}{\frac {n}{2(n+2)}}{\biggr ]}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{n+2}+1}}}\,\mathrm {d} x}
Im Folgenden werden einige singuläre elliptische Integralwerte hergeleitet:
Und die folgende Funktion hat die nachfolgende elliptische Stammfunktion:
1
x
8
+
1
=
d
d
x
1
4
sec
(
π
8
)
F
{
2
arctan
[
2
cos
(
π
/
8
)
x
x
4
+
2
x
2
+
1
−
x
2
+
1
]
;
2
2
4
sin
(
π
8
)
}
+
1
4
sec
(
π
8
)
F
{
arcsin
[
2
cos
(
π
/
8
)
x
x
2
+
1
]
;
tan
(
π
8
)
}
{\displaystyle {\frac {1}{\sqrt {x^{8}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}}
Für den Wert
n
=
6
{\displaystyle n=6}
1
8
2
4
csc
(
π
8
)
β
(
3
8
)
=
∫
0
∞
1
x
8
+
1
d
x
=
{\displaystyle {\frac {1}{8{\sqrt[{4}]{2}}}}\csc {\bigl (}{\frac {\pi }{8}}{\bigr )}\beta {\bigl (}{\frac {3}{8}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{8}+1}}}\,\mathrm {d} x=}
=
⟨
1
4
sec
(
π
8
)
F
{
2
arctan
[
2
cos
(
π
/
8
)
x
x
4
+
2
x
2
+
1
−
x
2
+
1
]
;
2
2
4
sin
(
π
8
)
}
+
1
4
sec
(
π
8
)
F
{
arcsin
[
2
cos
(
π
/
8
)
x
x
2
+
1
]
;
tan
(
π
8
)
}
⟩
x
=
0
x
=
∞
=
{\displaystyle ={\biggl \langle }{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}{\biggr \rangle }_{x=0}^{x=\infty }=}
=
1
4
sec
(
π
8
)
F
[
π
;
2
2
4
sin
(
π
8
)
]
=
1
2
sec
(
π
8
)
K
(
2
2
−
2
)
=
2
sin
(
π
8
)
K
(
2
−
1
)
{\displaystyle ={\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\bigl [}\pi ;2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\bigr ]}={\frac {1}{2}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2{\sqrt {2}}-2}}{\bigr )}=2\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2}}-1)}
Daraus folgt:
K
(
2
−
1
)
=
1
8
2
4
(
2
+
1
)
β
(
3
8
)
{\displaystyle {\color {ForestGreen}K({\sqrt {2}}-1)={\frac {1}{8}}{\sqrt[{4}]{2}}\,({\sqrt {2}}+1)\,\beta {\bigl (}{\frac {3}{8}}{\bigr )}}}
Diese wichtigen Werte hat die elliptische Nomenfunktion:
q
(
1
2
2
)
=
exp
(
−
π
)
{\displaystyle q({\tfrac {1}{2}}{\sqrt {2}})=\exp(-\pi )}
q
[
1
4
(
6
−
2
)
]
=
exp
(
−
3
π
)
{\displaystyle q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )}
q
(
2
−
1
)
=
exp
(
−
2
π
)
{\displaystyle q({\sqrt {2}}-1)=\exp(-{\sqrt {2}}\,\pi )}
Für den Beweis der Richtigkeit dieser Nomenwerte siehe den Artikel Elliptisches Nomen !
Basierend auf diesen Integralidentitäten und den oben genannten Modulidentitäten der Thetafunktionen im gleichnamigen Abschnitt dieses Artikels sollen nun exemplarische Theta-Nullwerte ermittelt werden:
ϑ
00
[
q
(
k
)
]
=
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[q(k)]={\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
exp
(
−
π
)
]
=
ϑ
00
[
q
(
1
2
2
)
]
=
2
π
−
1
K
(
1
2
2
)
=
2
−
1
/
2
π
−
1
/
2
β
(
1
4
)
1
/
2
=
2
−
1
/
4
π
4
Γ
(
3
4
)
−
1
{\displaystyle \vartheta _{00}[\exp(-\pi )]=\vartheta _{00}[q({\tfrac {1}{2}}{\sqrt {2}})]={\sqrt {2\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}}=2^{-1/2}\pi ^{-1/2}\beta ({\tfrac {1}{4}})^{1/2}=2^{-1/4}{\sqrt[{4}]{\pi }}\,{\Gamma {\bigl (}{\tfrac {3}{4}}{\bigr )}}^{-1}}
ϑ
00
[
exp
(
−
3
π
)
]
=
ϑ
00
{
q
[
1
4
(
6
−
2
)
]
}
=
2
π
−
1
K
[
1
4
(
6
−
2
)
]
=
2
−
1
/
6
3
−
1
/
8
π
−
1
/
2
β
(
1
3
)
1
/
2
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\vartheta _{00}{\bigl \{}q{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}{\bigr \}}={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}}=2^{-1/6}3^{-1/8}\pi ^{-1/2}\beta ({\tfrac {1}{3}})^{1/2}}
ϑ
00
[
exp
(
−
2
π
)
]
=
ϑ
00
[
q
(
2
−
1
)
]
=
2
π
−
1
K
(
2
−
1
)
=
2
−
1
/
8
cos
(
1
8
π
)
π
−
1
/
2
β
(
3
8
)
1
/
2
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {2}}\,\pi )]=\vartheta _{00}[q({\sqrt {2}}-1)]={\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/8}\cos({\tfrac {1}{8}}\pi )\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}
ϑ
01
[
q
(
k
)
]
=
1
−
k
2
4
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{01}[q(k)]={\sqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
01
[
exp
(
−
2
π
)
]
=
ϑ
01
[
q
(
2
−
1
)
]
=
2
2
−
2
4
2
π
−
1
K
(
2
−
1
)
=
2
−
1
/
4
cos
(
1
8
π
)
1
/
2
π
−
1
/
2
β
(
3
8
)
1
/
2
{\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=\vartheta _{01}[q({\sqrt {2}}-1)]={\sqrt[{4}]{2{\sqrt {2}}-2}}\,{\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/4}\cos({\tfrac {1}{8}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}
In der folgenden Tabelle werden die lemniskatisch beschaffenen Werte[ 23]
x
ϑ₁₀(x)
ϑ₀₀(x)
ϑ₁₀(x)²/ϑ₀₀(x)²
e
−
π
{\displaystyle {\text{e}}^{-\pi }}
π
4
Γ
(
3
4
)
−
1
2
−
1
/
4
=
G
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}={\sqrt {G}}}
π
4
Γ
(
3
4
)
−
1
=
2
1
/
4
G
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}=2^{1/4}{\sqrt {G}}}
λ*(1)
e
−
2
π
{\displaystyle {\text{e}}^{-2\pi }}
π
4
Γ
(
3
4
)
−
1
2
−
3
/
4
2
−
1
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}-1}}}
π
4
Γ
(
3
4
)
−
1
2
−
3
/
4
2
+
1
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}+1}}}
λ*(4)
e
−
3
π
{\displaystyle {\text{e}}^{-3\pi }}
π
4
Γ
(
3
4
)
−
1
2
−
3
/
2
3
−
3
/
8
3
−
1
(
3
+
1
−
12
4
)
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}})}
π
4
Γ
(
3
4
)
−
1
2
−
1
/
4
3
−
3
/
8
3
+
1
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{-3/8}{\sqrt {{\sqrt {3}}+1}}}
λ*(9)
e
−
4
π
{\displaystyle {\text{e}}^{-4\pi }}
π
4
Γ
(
3
4
)
−
1
2
−
5
/
4
(
2
4
−
1
)
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}-1)}
π
4
Γ
(
3
4
)
−
1
2
−
5
/
4
(
2
4
+
1
)
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}+1)}
λ*(16)
e
−
5
π
{\displaystyle {\text{e}}^{-5\pi }}
π
4
Γ
(
3
4
)
−
1
2
−
5
/
4
5
−
1
/
2
(
5
4
−
1
)
2
Φ
−
1
/
2
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}5^{-1/2}({\sqrt[{4}]{5}}-1)^{2}\Phi ^{-1/2}}
π
4
Γ
(
3
4
)
−
1
5
−
1
/
2
Φ
3
/
2
{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}}
λ*(25)
Weitere Werte für ϑ₀₀(x):
ϑ
00
(
e
−
6
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
2
3
−
3
/
8
cot
(
1
24
π
)
(
3
4
+
1
)
(
3
+
1
−
12
4
)
{\displaystyle \vartheta _{00}({\text{e}}^{-6\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})}
ϑ
00
(
e
−
7
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
5
/
8
7
−
7
/
16
3
+
7
4
5
−
7
+
28
4
{\displaystyle \vartheta _{00}({\text{e}}^{-7\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}}
ϑ
00
(
e
−
8
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
2
(
2
+
2
+
2
7
/
8
)
{\displaystyle \vartheta _{00}({\text{e}}^{-8\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}({\sqrt {2+{\sqrt {2}}}}+2^{7/8})}
ϑ
00
(
e
−
9
π
)
=
π
4
Γ
(
3
4
)
−
1
3
−
1
(
2
3
+
2
3
+
1
)
{\displaystyle \vartheta _{00}({\text{e}}^{-9\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)}
ϑ
00
(
e
−
10
π
)
=
π
4
Γ
(
3
4
)
−
1
5
−
1
/
2
Φ
3
/
2
cos
[
1
4
arcsin
(
Φ
−
12
)
]
{\displaystyle \vartheta _{00}({\text{e}}^{-10\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}\cos {\bigl [}{\tfrac {1}{4}}\arcsin {\bigl (}\Phi ^{-12}{\bigr )}{\bigr ]}}
ϑ
00
(
e
−
11
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
5
/
4
11
−
5
/
8
11
+
3
{
4
+
11
−
3
3
tanh
[
1
4
arcosh
(
7
4
)
+
1
2
artanh
(
4
9
3
)
−
1
6
artanh
(
1
27
3
)
]
}
{\displaystyle \vartheta _{00}({\text{e}}^{-11\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}11^{-5/8}{\sqrt {{\sqrt {11}}+3}}\,{\bigl \{}4+{\sqrt {11}}-3{\sqrt {3}}\tanh {\bigl [}{\tfrac {1}{4}}\operatorname {arcosh} ({\tfrac {7}{4}})+{\tfrac {1}{2}}\operatorname {artanh} ({\tfrac {4}{9}}{\sqrt {3}})-{\tfrac {1}{6}}\operatorname {artanh} ({\tfrac {1}{27}}{\sqrt {3}}){\bigr ]}{\bigr \}}}
ϑ
00
(
e
−
12
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
2
3
−
3
/
8
cot
(
1
24
π
)
(
3
4
+
1
)
(
3
+
1
−
12
4
)
cos
{
1
2
arcsin
[
1
2
(
2
+
3
)
(
3
−
2
)
2
(
2
−
1
)
2
(
3
4
−
1
)
4
]
}
{\displaystyle \vartheta _{00}({\text{e}}^{-12\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})\cos {\bigl \{}{\tfrac {1}{2}}\arcsin {\bigl [}{\tfrac {1}{2}}(2+{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})^{2}({\sqrt {2}}-1)^{2}({\sqrt[{4}]{3}}-1)^{4}{\bigr ]}{\bigr \}}}
ϑ
00
(
e
−
13
π
)
=
π
4
Γ
(
3
4
)
−
1
13
−
1
/
2
5
13
+
18
{
1
6
(
5
39
−
17
3
)
coth
[
1
3
artanh
(
6
11
3
)
−
1
2
arcosh
(
4
13
13
)
]
−
1
2
(
13
−
3
)
}
{\displaystyle \vartheta _{00}({\text{e}}^{-13\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}13^{-1/2}{\sqrt {5{\sqrt {13}}+18}}\,{\bigl \{}{\tfrac {1}{6}}(5{\sqrt {39}}-17{\sqrt {3}})\coth {\bigl [}{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {6}{11}}{\sqrt {3}})-{\tfrac {1}{2}}\operatorname {arcosh} {\bigl (}{\tfrac {4}{13}}{\sqrt {13}}{\bigr )}{\bigr ]}-{\tfrac {1}{2}}({\sqrt {13}}-3){\bigr \}}}
ϑ
00
(
e
−
14
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
5
/
8
7
−
7
/
16
3
+
7
4
5
−
7
+
28
4
cos
{
1
4
arcsin
[
(
1
4
14
+
1
4
2
−
1
2
7
4
)
12
]
}
{\displaystyle \vartheta _{00}({\text{e}}^{-14\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}\,\cos {\bigl \{}{\tfrac {1}{4}}\arcsin {\bigl [}({\tfrac {1}{4}}{\sqrt {14}}+{\tfrac {1}{4}}{\sqrt {2}}-{\tfrac {1}{2}}{\sqrt[{4}]{7}})^{12}{\bigr ]}{\bigr \}}}
ϑ
00
(
e
−
15
π
)
=
π
4
Γ
(
3
4
)
−
1
3
−
1
/
2
5
−
1
/
2
Φ
3
/
2
(
2
1
+
Φ
−
8
+
Φ
−
16
+
2
+
Φ
−
8
+
1
−
Φ
−
8
)
1
/
2
{\displaystyle \vartheta _{00}({\text{e}}^{-15\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1/2}5^{-1/2}\Phi ^{3/2}{\bigl (}{\sqrt {2{\sqrt {1+\Phi ^{-8}+\Phi ^{-16}}}+2+\Phi ^{-8}}}+{\sqrt {1-\Phi ^{-8}}}{\bigr )}^{1/2}}
ϑ
00
(
e
−
16
π
)
=
π
4
Γ
(
3
4
)
−
1
[
2
−
9
/
4
(
2
4
+
1
)
+
2
−
23
/
16
2
+
1
4
]
{\displaystyle \vartheta _{00}({\text{e}}^{-16\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}{\bigl [}2^{-9/4}({\sqrt[{4}]{2}}+1)+2^{-23/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\bigr ]}}
ϑ
00
(
e
−
17
π
)
=
π
4
Γ
(
3
4
)
−
1
2
−
3
/
2
17
−
1
/
2
[
(
17
4
+
1
)
17
−
1
+
272
8
17
+
3
]
{\displaystyle \vartheta _{00}({\text{e}}^{-17\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}17^{-1/2}{\bigl [}({\sqrt[{4}]{17}}+1){\sqrt {{\sqrt {17}}-1}}+{\sqrt[{8}]{272}}{\sqrt {{\sqrt {17}}+3}}{\bigr ]}}
ϑ
00
(
e
−
18
π
)
=
π
4
Γ
(
3
4
)
−
1
3
−
1
(
2
3
+
2
3
+
1
)
cos
⟨
1
4
arcsin
{
[
2
3
−
3
−
6
(
2
−
3
)
5
/
6
+
2
(
2
−
3
)
7
/
6
]
4
}
⟩
{\displaystyle \vartheta _{00}({\text{e}}^{-18\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)\cos {\bigl \langle }{\tfrac {1}{4}}\arcsin {\bigl \{}{\bigl [}2{\sqrt {3}}-3-{\sqrt {6}}(2-{\sqrt {3}})^{5/6}+{\sqrt {2}}(2-{\sqrt {3}})^{7/6}{\bigr ]}^{4}{\bigr \}}{\bigr \rangle }}
Hierbei steht
G
{\displaystyle G}
lemniskatische Konstante dividiert durch die Kreiszahl ist. Die soeben abgebildeten Werte wurden durch den südkoreanischen Mathematiker Jinhee Yi aus der Nationaluniversität Busan (부산 대학교) erforscht. Seine Resultate wurden anschließend im Journal of Mathematical Analysis and Applications
Außerdem gilt:
ϑ
00
[
exp
(
−
1
2
π
)
]
=
π
4
Γ
(
3
4
)
−
1
2
−
1
/
4
2
+
1
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{2}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}{\sqrt {{\sqrt {2}}+1}}}
ϑ
00
[
exp
(
−
1
3
π
)
]
=
π
4
Γ
(
3
4
)
−
1
2
−
1
/
4
3
1
/
8
3
+
1
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{3}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{1/8}{\sqrt {{\sqrt {3}}+1}}}
Diese beiden Werte können direkt mit der Poissonschen Summenformel ermittelt werden:
ϑ
00
[
exp
(
−
π
/
y
)
]
=
y
ϑ
00
[
exp
(
−
π
y
)
]
{\displaystyle \vartheta _{00}[\exp(-\pi /y)]={\sqrt {y}}\,\vartheta _{00}[\exp(-\pi y)]}
Wenn der Kehrwert der Gelfondschen Konstante mit dem Kehrwert einer ungeraden Zahl potenziert wird, dann entstehen Werte mit zugehörigen Thetafunktionswerten, die mit Hilfe des hyperbolisch lemniskatischen Sinus stark vereinfacht dargestellt werden können:
ϑ
00
[
exp
(
−
1
5
π
)
]
=
π
4
Γ
(
3
4
)
−
1
slh
(
1
5
2
ϖ
)
slh
(
2
5
2
ϖ
)
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{5}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}}
ϑ
00
[
exp
(
−
1
7
π
)
]
=
π
4
Γ
(
3
4
)
−
1
slh
(
1
7
2
ϖ
)
slh
(
2
7
2
ϖ
)
slh
(
3
7
2
ϖ
)
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{7}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}}
ϑ
00
[
exp
(
−
1
9
π
)
]
=
π
4
Γ
(
3
4
)
−
1
slh
(
1
9
2
ϖ
)
slh
(
2
9
2
ϖ
)
slh
(
3
9
2
ϖ
)
slh
(
4
9
2
ϖ
)
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{9}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}}
ϑ
00
[
exp
(
−
1
11
π
)
]
=
π
4
Γ
(
3
4
)
−
1
slh
(
1
11
2
ϖ
)
slh
(
2
11
2
ϖ
)
slh
(
3
11
2
ϖ
)
slh
(
4
11
2
ϖ
)
slh
(
5
11
2
ϖ
)
{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{11}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}}
Diese äquianharmonischen Funktionswerte hat die Funktion ϑ₀₀:
ϑ
00
[
exp
(
−
3
π
)
]
=
π
−
1
/
2
2
−
1
/
6
3
−
1
/
8
β
(
1
3
)
1
/
2
=
2
1
/
3
3
1
/
8
ω
2
/
π
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}=2^{1/3}3^{1/8}{\sqrt {\omega _{2}/\pi }}}
ϑ
00
[
exp
(
−
2
3
π
)
]
=
π
−
1
/
2
2
−
1
/
6
3
−
1
/
8
β
(
1
3
)
1
/
2
cos
(
1
24
π
)
{\displaystyle \vartheta _{00}[\exp(-2{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}\cos({\tfrac {1}{24}}\pi )}
ϑ
00
[
exp
(
−
3
3
π
)
]
=
π
−
1
/
2
2
−
1
/
6
3
−
7
/
8
β
(
1
3
)
1
/
2
(
2
3
+
1
)
{\displaystyle \vartheta _{00}[\exp(-3{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-7/8}\beta ({\tfrac {1}{3}})^{1/2}({\sqrt[{3}]{2}}+1)}
ϑ
00
[
exp
(
−
4
3
π
)
]
=
π
−
1
/
2
2
−
7
/
6
3
−
1
/
8
β
(
1
3
)
1
/
2
[
1
+
cos
(
1
12
π
)
]
{\displaystyle \vartheta _{00}[\exp(-4{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-7/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}[1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}]}
ϑ
00
[
exp
(
−
5
3
π
)
]
=
π
−
1
/
2
2
−
1
/
6
3
−
9
/
8
β
(
1
3
)
1
/
2
sin
(
1
5
π
)
(
2
5
100
3
+
2
5
10
3
+
3
5
5
+
1
)
{\displaystyle \vartheta _{00}[\exp(-5{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-9/8}\beta ({\tfrac {1}{3}})^{1/2}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)}
Dabei ist
ω
2
{\displaystyle \omega _{2}}
Omega-2-Konstante des äquianharmonischen Falls.
Einige äquianharmonischen Thetafunktionswerte[ 24] Bruce Berndt und Örs Rebák erforscht.
Funktionswerte der Form ϑ₀₁:
ϑ
01
[
exp
(
−
2
π
)
]
=
2
−
1
/
4
π
−
1
/
2
cos
(
1
8
π
)
β
(
3
8
)
{\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}}
ϑ
01
[
exp
(
−
3
2
π
)
]
=
2
−
1
/
4
3
−
1
/
2
π
−
1
/
2
cos
(
1
8
π
)
β
(
3
8
)
3
+
2
{\displaystyle \vartheta _{01}[\exp(-3{\sqrt {2}}\,\pi )]=2^{-1/4}3^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {{\sqrt {3}}+{\sqrt {2}}}}}
ϑ
01
[
exp
(
−
1
3
2
π
)
]
=
2
−
1
/
4
π
−
1
/
2
cos
(
1
8
π
)
β
(
3
8
)
3
−
2
{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{3}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {{\sqrt {3}}-{\sqrt {2}}}}}
ϑ
01
[
exp
(
−
5
2
π
)
]
=
2
−
1
/
4
5
−
1
/
2
π
−
1
/
2
cos
(
1
8
π
)
β
(
3
8
)
2
g
(
50
)
+
1
{\displaystyle \vartheta _{01}[\exp(-5{\sqrt {2}}\,\pi )]=2^{-1/4}5^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {2{\text{g}}(50)+1}}}
ϑ
01
[
exp
(
−
1
5
2
π
)
]
=
2
−
1
/
4
π
−
1
/
2
cos
(
1
8
π
)
β
(
3
8
)
1
−
2
g
(
50
)
−
1
{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{5}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {1-2{\text{g}}(50)^{-1}}}}
Wichtige Konstante
g
(
50
)
{\displaystyle {\text{g}}(50)}
g
(
50
)
=
w
R
5
(
2
−
1
)
=
2
[
exp
(
−
5
2
π
)
;
exp
(
−
10
2
π
)
]
∞
[
exp
(
−
2
π
)
;
exp
(
−
2
2
π
)
]
∞
−
5
=
{\displaystyle {\text{g}}(50)=w_{R5}({\sqrt {2}}-1)=2\,[\exp(-5\,{\sqrt {2}}\,\pi );\exp(-10\,{\sqrt {2}}\,\pi )]_{\infty }[\exp(-{\sqrt {2}}\,\pi );\exp(-2\,{\sqrt {2}}\,\pi )]_{\infty }^{-5}=}
=
1
2
{
4
3
2
cos
(
1
10
π
)
cosh
[
1
3
artanh
(
3
8
6
)
]
+
1
3
tan
(
1
5
π
)
}
2
−
1
2
=
{\displaystyle ={\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}^{2}-{\tfrac {1}{2}}=}
=
⟨
1
2
−
1
2
{
4
3
2
sin
(
1
5
π
)
cosh
[
1
3
artanh
(
3
8
6
)
]
−
1
3
cot
(
1
10
π
)
}
2
⟩
−
1
=
{\displaystyle ={\bigl \langle }{\tfrac {1}{2}}-{\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}^{2}{\bigr \rangle }^{-1}=}
=
Φ
−
1
cot
[
1
4
π
−
arctan
(
1
3
5
−
1
3
6
30
+
4
5
3
+
1
3
6
30
−
4
5
3
)
]
=
{\displaystyle =\Phi ^{-1}\cot {\bigl [}{\tfrac {1}{4}}\pi -\arctan {\bigl (}{\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}{\bigr )}{\bigr ]}=}
≈
2,121
90403802900202926
{\displaystyle \approx 2{,}12190403802900202926}
Zugehörige Gleichungen:
g
(
50
)
6
−
2
g
(
50
)
5
−
2
g
(
50
)
−
1
=
0
{\displaystyle {\text{g}}(50)^{6}-2\,{\text{g}}(50)^{5}-2\,{\text{g}}(50)-1=0}
g
(
50
)
3
−
g
(
50
)
2
−
Φ
g
(
50
)
−
Φ
=
0
{\displaystyle {\text{g}}(50)^{3}-{\text{g}}(50)^{2}-\Phi \,{\text{g}}(50)-\Phi =0}
Diese Konstante spielt in der Galois-Theorie eine wichtige Rolle.
Mit dieser Konstante wird hierbei der Ramanujansche g-Funktionswert
g
(
50
)
{\displaystyle g(50)}
Und mit dem griechischen Buchstaben
Φ
=
5
+
1
2
{\displaystyle \Phi ={\tfrac {{\sqrt {5}}+1}{2}}}
goldene Zahl dargestellt.
Als Singuläre elliptische Integralwerte und im englischen Sprachraum als Elliptic Integral Singular Values werden diejenigen vollständigen elliptischen Integrale[ 25]
ϑ
00
[
exp
(
−
5
π
)
]
=
2
π
−
1
K
{
sin
[
1
2
arcsin
(
5
−
2
)
]
}
=
2
−
17
/
40
5
−
5
/
16
(
5
+
1
)
5
/
8
cos
(
1
20
π
)
1
/
2
π
−
1
/
2
β
(
9
20
)
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {5}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl \{}\sin {\bigl [}{\tfrac {1}{2}}\arcsin({\sqrt {5}}-2){\bigr ]}{\bigr \}}}}=2^{-17/40}5^{-5/16}({\sqrt {5}}+1)^{5/8}\cos({\tfrac {1}{20}}\pi )^{1/2}\pi ^{-1/2}{\sqrt {\beta ({\tfrac {9}{20}})}}}
ϑ
00
[
exp
(
−
7
π
)
]
=
2
π
−
1
K
[
1
8
(
3
2
−
14
)
]
=
2
−
2
/
7
7
−
5
/
8
cot
(
1
7
π
)
1
/
2
π
−
1
β
(
2
7
)
β
(
4
7
)
β
(
5
14
)
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {7}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{8}}(3{\sqrt {2}}-{\sqrt {14}}){\bigr ]}}}=2^{-2/7}7^{-5/8}\cot({\tfrac {1}{7}}\pi )^{1/2}\,\pi ^{-1}{\sqrt {\beta ({\tfrac {2}{7}})\beta ({\tfrac {4}{7}})\beta ({\tfrac {5}{14}})}}}
ϑ
00
[
exp
(
−
15
π
)
]
=
2
π
−
1
K
[
1
16
(
10
−
6
)
(
3
−
5
)
(
2
−
3
)
]
=
2
−
3
/
2
3
−
5
/
8
5
−
5
/
8
(
5
+
1
)
π
−
1
β
(
2
15
)
β
(
8
15
)
β
(
1
3
)
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {15}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{16}}({\sqrt {10}}-{\sqrt {6}})(3-{\sqrt {5}})(2-{\sqrt {3}}){\bigr ]}}}=2^{-3/2}3^{-5/8}5^{-5/8}({\sqrt {5}}+1)\,\pi ^{-1}{\sqrt {\beta ({\tfrac {2}{15}})\beta ({\tfrac {8}{15}})\beta ({\tfrac {1}{3}})}}}
Folgender Funktionswert kann nicht mit der reduzierten Betafunktion als einzige nicht elementare Funktion dargestellt werden:
ϑ
00
[
exp
(
−
11
π
)
]
=
2
π
−
1
K
{
sin
[
1
2
arcsin
(
1
2
T
T
R
I
−
4
)
]
}
=
2
9
/
22
11
−
3
/
8
π
−
1
/
2
(
T
T
R
I
2
−
T
T
R
I
)
cos
(
1
22
π
)
cos
(
3
22
π
)
B
(
5
22
;
15
22
)
{\displaystyle \vartheta _{00}[\exp(-{\sqrt {11}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl \{}\sin {\bigl [}{\tfrac {1}{2}}\arcsin({\tfrac {1}{2}}T_{TRI}^{-4}){\bigr ]}{\bigr \}}}}={2}^{9/22}{11}^{-3/8}{\pi }^{-1/2}(T_{TRI}^{2}-{T_{TRI}}){\sqrt {\cos({\tfrac {1}{22}}\pi )\cos({\tfrac {3}{22}}\pi )\mathrm {B} ({\tfrac {5}{22}};{\tfrac {15}{22}})}}}
Mit der genannten Bezeichnung wird die Tribonacci-Konstante dargestellt:
T
T
R
I
=
1
3
19
+
3
33
3
+
1
3
19
−
3
33
3
+
1
3
=
1
2
(
2
3
+
1
3
3
33
+
17
3
−
1
3
3
33
−
17
3
)
3
{\displaystyle T_{TRI}={\tfrac {1}{3}}{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\tfrac {1}{3}}={\tfrac {1}{2}}{\bigl (}{\tfrac {2}{3}}+{\tfrac {1}{3}}{\sqrt[{3}]{3{\sqrt {33}}+17}}-{\tfrac {1}{3}}{\sqrt[{3}]{3{\sqrt {33}}-17}}{\bigr )}^{3}}
T
T
R
I
3
−
T
T
R
I
2
−
T
T
R
I
−
1
=
0
{\displaystyle T_{TRI}^{3}-T_{TRI}^{2}-T_{TRI}-1=0}
Und für die erweiterte Eulersche Betafunktion gilt diese Definition:
B
(
a
;
b
)
=
Γ
(
a
)
Γ
(
b
)
/
Γ
(
a
+
b
)
{\displaystyle \mathrm {B} (a;b)=\Gamma (a)\Gamma (b)/\Gamma (a+b)}
Die Hauptthetanullwert-Ableitungsfunktion ϑ'₀₀(x) ist die Ableitung der Funktion ϑ₀₀(x) bezüglich des Nomens x:
ϑ
00
′
(
x
)
=
d
d
x
ϑ
00
(
x
)
{\displaystyle \vartheta '_{00}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{00}(x)}
ϑ
00
′
(
x
)
=
2
+
∑
n
=
1
∞
2
(
n
+
1
)
2
x
n
(
n
+
2
)
{\displaystyle \vartheta '_{00}(x)=2+\sum _{n=1}^{\infty }2(n+1)^{2}x^{n(n+2)}}
Diese Identität hat die Hauptthetanullwert-Ableitungsfunktion in Bezug auf das vollständige elliptische Integral zweiter Art:
ϑ
00
′
(
x
)
=
ϑ
00
(
x
)
[
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
{
1
2
π
x
E
[
ϑ
00
(
x
)
2
−
ϑ
01
(
x
)
2
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
−
ϑ
01
(
x
)
2
4
x
}
{\displaystyle \vartheta '_{00}(x)=\vartheta _{00}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{01}(x)^{2}}{4x}}{\biggr \}}}
Und folgende Werte hat diese Funktion:
ϑ
00
′
(
e
−
π
)
=
e
π
G
2
8
4
π
{\displaystyle \vartheta '_{00}({\text{e}}^{-\pi })={\frac {{\text{e}}^{\pi }{\sqrt {G}}}{2{\sqrt[{4}]{8}}\,\pi }}}
ϑ
00
′
(
e
−
π
/
2
)
=
cos
(
1
8
π
)
e
π
/
2
G
[
(
2
−
1
)
π
G
2
+
1
]
2
4
π
{\displaystyle \vartheta '_{00}({\text{e}}^{-\pi /2})={\frac {\cos({\tfrac {1}{8}}\pi ){\text{e}}^{\pi /2}{\sqrt {G}}[({\sqrt {2}}-1)\pi G^{2}+1]}{{\sqrt[{4}]{2}}\,\pi }}}
Diese Werte spielen insbesondere in der Theorie über die elliptische Alphafunktion[ 26] [ 27]
Zu den Transformationen des Nomens[ 28]
ϑ
10
(
x
2
)
=
1
2
2
[
ϑ
00
(
x
)
2
−
ϑ
01
(
x
)
2
]
{\displaystyle \vartheta _{10}(x^{2})={\tfrac {1}{2}}{\sqrt {2[\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}]}}}
ϑ
00
(
x
2
)
=
1
2
2
[
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
{\displaystyle \vartheta _{00}(x^{2})={\tfrac {1}{2}}{\sqrt {2[\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}]}}}
ϑ
01
(
x
2
)
=
ϑ
01
(
x
)
ϑ
00
(
x
)
{\displaystyle \vartheta _{01}(x^{2})={\sqrt {\vartheta _{01}(x)\vartheta _{00}(x)}}}
Nach der Jacobi-Identität werden somit auch durch die Quadrate der drei Theta-Nullwertfunktionen von der Quadratfunktion als innere Funktion pythagoräische Tripel gebildet. Außerdem gelten jene Transformationen:
ϑ
00
(
x
4
)
=
1
2
ϑ
00
(
x
)
+
1
2
ϑ
01
(
x
)
{\displaystyle \vartheta _{00}(x^{4})={\tfrac {1}{2}}\vartheta _{00}(x)+{\tfrac {1}{2}}\vartheta _{01}(x)}
27
ϑ
00
(
x
3
)
8
−
18
ϑ
00
(
x
3
)
4
ϑ
00
(
x
)
4
−
ϑ
00
(
x
)
8
=
8
ϑ
00
(
x
3
)
2
ϑ
00
(
x
)
2
[
2
ϑ
01
(
x
)
4
−
ϑ
00
(
x
)
4
]
{\displaystyle 27\,\vartheta _{00}(x^{3})^{8}-18\,\vartheta _{00}(x^{3})^{4}\vartheta _{00}(x)^{4}-\,\vartheta _{00}(x)^{8}=8\,\vartheta _{00}(x^{3})^{2}\vartheta _{00}(x)^{2}[2\,\vartheta _{01}(x)^{4}-\vartheta _{00}(x)^{4}]}
27
ϑ
01
(
x
3
)
8
−
18
ϑ
01
(
x
3
)
4
ϑ
01
(
x
)
4
−
ϑ
01
(
x
)
8
=
8
ϑ
01
(
x
3
)
2
ϑ
01
(
x
)
2
[
2
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
]
{\displaystyle 27\,\vartheta _{01}(x^{3})^{8}-18\,\vartheta _{01}(x^{3})^{4}\vartheta _{01}(x)^{4}-\,\vartheta _{01}(x)^{8}=8\,\vartheta _{01}(x^{3})^{2}\vartheta _{01}(x)^{2}[2\,\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}
[
ϑ
00
(
x
)
2
−
ϑ
00
(
x
5
)
2
]
[
5
ϑ
00
(
x
5
)
2
−
ϑ
00
(
x
)
2
]
5
=
256
ϑ
00
(
x
5
)
2
ϑ
00
(
x
)
2
ϑ
01
(
x
)
4
[
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
]
{\displaystyle [\vartheta _{00}(x)^{2}-\vartheta _{00}(x^{5})^{2}][5\,\vartheta _{00}(x^{5})^{2}-\vartheta _{00}(x)^{2}]^{5}=256\,\vartheta _{00}(x^{5})^{2}\vartheta _{00}(x)^{2}\vartheta _{01}(x)^{4}[\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}
[
ϑ
01
(
x
5
)
2
−
ϑ
01
(
x
)
2
]
[
5
ϑ
01
(
x
5
)
2
−
ϑ
01
(
x
)
2
]
5
=
256
ϑ
01
(
x
5
)
2
ϑ
01
(
x
)
2
ϑ
00
(
x
)
4
[
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
]
{\displaystyle [\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}][5\,\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}]^{5}=256\,\vartheta _{01}(x^{5})^{2}\vartheta _{01}(x)^{2}\vartheta _{00}(x)^{4}[\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}
Die Formeln für die Theta-Nullwert-Funktionswerte von der Kubikwurzel des elliptischen Nomens kommen durch die Gegenüberstellung der beiden reellen Lösung der korrespondierenden quartischen Gleichungen hervor:
[
ϑ
00
(
x
1
/
3
)
2
ϑ
00
(
x
)
2
−
3
ϑ
00
(
x
3
)
2
ϑ
00
(
x
)
2
]
2
=
4
−
4
[
2
ϑ
10
(
x
)
2
ϑ
01
(
x
)
2
ϑ
00
(
x
)
4
]
2
/
3
{\displaystyle {\biggl [}{\frac {\vartheta _{00}(x^{1/3})^{2}}{\vartheta _{00}(x)^{2}}}-{\frac {3\,\vartheta _{00}(x^{3})^{2}}{\vartheta _{00}(x)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\vartheta _{10}(x)^{2}\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{4}}}{\biggr ]}^{2/3}}
[
3
ϑ
01
(
x
3
)
2
ϑ
01
(
x
)
2
−
ϑ
01
(
x
1
/
3
)
2
ϑ
01
(
x
)
2
]
2
=
4
+
4
[
2
ϑ
10
(
x
)
2
ϑ
00
(
x
)
2
ϑ
01
(
x
)
4
]
2
/
3
{\displaystyle {\biggl [}{\frac {3\,\vartheta _{01}(x^{3})^{2}}{\vartheta _{01}(x)^{2}}}-{\frac {\vartheta _{01}(x^{1/3})^{2}}{\vartheta _{01}(x)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\vartheta _{10}(x)^{2}\vartheta _{00}(x)^{2}}{\vartheta _{01}(x)^{4}}}{\biggr ]}^{2/3}}
Auf folgende Weise kann der Rogers-Ramanujan-Kettenbruch in Abhängigkeit von der Jacobischen Thetafunktion definiert werden:
R
(
x
)
=
tan
{
1
2
arctan
[
1
2
−
ϑ
01
(
x
)
2
2
ϑ
01
(
x
5
)
2
]
}
1
/
5
tan
{
1
2
arccot
[
1
2
−
ϑ
01
(
x
)
2
2
ϑ
01
(
x
5
)
2
]
}
2
/
5
{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}
R
(
x
2
)
=
tan
{
1
2
arctan
[
1
2
−
ϑ
01
(
x
)
2
2
ϑ
01
(
x
5
)
2
]
}
2
/
5
cot
{
1
2
arccot
[
1
2
−
ϑ
01
(
x
)
2
2
ϑ
01
(
x
5
)
2
]
}
1
/
5
{\displaystyle R(x^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}
R
(
x
2
)
=
tan
{
1
2
arctan
[
ϑ
00
(
x
)
2
2
ϑ
00
(
x
5
)
2
−
1
2
]
}
2
/
5
tan
{
1
2
arccot
[
ϑ
00
(
x
)
2
2
ϑ
00
(
x
5
)
2
−
1
2
]
}
1
/
5
{\displaystyle R(x^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}}
Die alternierende Rogers-Ramanujan-Kettenbruchfunktion S(x) hat die nachfolgenden beiden Identitäten:
S
(
x
)
=
R
(
x
4
)
R
(
x
2
)
R
(
x
)
=
tan
{
1
2
arctan
[
ϑ
00
(
x
)
2
2
ϑ
00
(
x
5
)
2
−
1
2
]
}
1
/
5
cot
{
1
2
arccot
[
ϑ
00
(
x
)
2
2
ϑ
00
(
x
5
)
2
−
1
2
]
}
2
/
5
{\displaystyle S(x)={\frac {R(x^{4})}{R(x^{2})R(x)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}}
Die Thetafunktionswerte von der fünften Wurzel des Nomens können als rationale Kombination der Kettenbrüche R und S und der Thetafunktionswerte von der fünften Potenz des Nomens und vom Nomen selbst dargestellt werden. Die nun folgenden vier Gleichungen sind für alle Werte x zwischen 0 und 1 gültig:
ϑ
00
(
x
1
/
5
)
ϑ
00
(
x
5
)
−
1
=
1
S
(
x
)
[
S
(
x
)
2
+
R
(
x
2
)
]
[
1
+
R
(
x
2
)
S
(
x
)
]
{\displaystyle {\frac {\vartheta _{00}(x^{1/5})}{\vartheta _{00}(x^{5})}}-1={\frac {1}{S(x)}}[S(x)^{2}+R(x^{2})][1+R(x^{2})S(x)]}
1
−
ϑ
01
(
x
1
/
5
)
ϑ
01
(
x
5
)
=
1
R
(
x
)
[
R
(
x
2
)
+
R
(
x
)
2
]
[
1
−
R
(
x
2
)
R
(
x
)
]
{\displaystyle 1-{\frac {\vartheta _{01}(x^{1/5})}{\vartheta _{01}(x^{5})}}={\frac {1}{R(x)}}[R(x^{2})+R(x)^{2}][1-R(x^{2})R(x)]}
Folgende Tangenssummen und Tangensdifferenzen sind gültig:
ϑ
00
(
x
1
/
5
)
2
−
ϑ
00
(
x
)
2
5
ϑ
00
(
x
5
)
2
−
ϑ
00
(
x
)
2
=
S
(
x
)
⊕
R
(
x
2
)
{\displaystyle {\frac {\vartheta _{00}(x^{1/5})^{2}-\vartheta _{00}(x)^{2}}{5\,\vartheta _{00}(x^{5})^{2}-\vartheta _{00}(x)^{2}}}=S(x)\oplus R(x^{2})}
ϑ
01
(
x
)
2
−
ϑ
01
(
x
1
/
5
)
2
5
ϑ
01
(
x
5
)
2
−
ϑ
01
(
x
)
2
=
R
(
x
)
⊖
R
(
x
2
)
{\displaystyle {\frac {\vartheta _{01}(x)^{2}-\vartheta _{01}(x^{1/5})^{2}}{5\,\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}}}=R(x)\ominus R(x^{2})}
Weiter gilt für alle Werte
0
<
x
<
1
{\displaystyle 0<x<1}
[
ϑ
00
(
x
1
/
5
)
2
ϑ
00
(
x
)
2
−
1
]
[
ϑ
10
(
x
1
/
5
)
ϑ
01
(
x
1
/
5
)
ϑ
10
(
x
)
ϑ
01
(
x
)
+
1
]
=
4
{\displaystyle {\biggl [}{\frac {\vartheta _{00}(x^{1/5})^{2}}{\vartheta _{00}(x)^{2}}}-1{\biggr ]}{\biggl [}{\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{01}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{01}(x)}}+1{\biggr ]}=4}
[
1
−
ϑ
01
(
x
1
/
5
)
2
ϑ
01
(
x
)
2
]
[
ϑ
10
(
x
1
/
5
)
ϑ
00
(
x
1
/
5
)
ϑ
10
(
x
)
ϑ
00
(
x
)
−
1
]
=
4
{\displaystyle {\biggl [}1-{\frac {\vartheta _{01}(x^{1/5})^{2}}{\vartheta _{01}(x)^{2}}}{\biggr ]}{\biggl [}{\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{00}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{00}(x)}}-1{\biggr ]}=4}
Daraus folgt:
ϑ
10
(
x
1
/
5
)
ϑ
01
(
x
1
/
5
)
ϑ
10
(
x
)
ϑ
01
(
x
)
+
1
=
4
ϑ
00
(
x
5
)
2
5
ϑ
00
(
x
5
)
2
−
ϑ
00
(
x
)
2
[
−
1
+
S
(
x
)
R
(
x
2
)
+
R
(
x
2
)
S
(
x
)
+
1
R
(
x
2
)
−
1
S
(
x
)
2
−
R
(
x
2
)
−
S
(
x
)
2
]
{\displaystyle {\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{01}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{01}(x)}}+1={\frac {4\,\vartheta _{00}(x^{5})^{2}}{5\,\vartheta _{00}(x^{5})^{2}-\vartheta _{00}(x)^{2}}}{\biggl [}-1+{\frac {S(x)}{R(x^{2})}}+{\frac {R(x^{2})}{S(x)}}+{\frac {1}{R(x^{2})}}-{\frac {1}{S(x)^{2}}}-R(x^{2})-S(x)^{2}{\biggr ]}}
ϑ
10
(
x
1
/
5
)
ϑ
00
(
x
1
/
5
)
ϑ
10
(
x
)
ϑ
00
(
x
)
−
1
=
4
ϑ
01
(
x
5
)
2
5
ϑ
01
(
x
5
)
2
−
ϑ
01
(
x
)
2
[
1
+
R
(
x
)
R
(
x
2
)
+
R
(
x
2
)
R
(
x
)
−
1
R
(
x
2
)
+
1
R
(
x
)
2
+
R
(
x
2
)
+
R
(
x
)
2
]
{\displaystyle {\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{00}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{00}(x)}}-1={\frac {4\,\vartheta _{01}(x^{5})^{2}}{5\,\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}}}{\biggl [}1+{\frac {R(x)}{R(x^{2})}}+{\frac {R(x^{2})}{R(x)}}-{\frac {1}{R(x^{2})}}+{\frac {1}{R(x)^{2}}}+R(x^{2})+R(x)^{2}{\biggr ]}}
In Kombination mit der elliptischen Nomenfunktion in Abhängigkeit vom elliptischen Modul k können diese Theoreme aufgestellt werden:
Die Nomenquadraturtheoreme der Funktionen ϑ₀₀ und ϑ₀₁ lauten wie folgt:
ϑ
01
[
q
(
k
)
]
=
ϑ
01
[
q
(
k
)
2
]
1
−
k
2
8
{\displaystyle \vartheta _{01}[q(k)]=\vartheta _{01}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}}
ϑ
01
[
q
(
k
)
2
]
=
ϑ
00
[
q
(
k
)
]
1
−
k
2
8
{\displaystyle \vartheta _{01}[q(k)^{2}]=\vartheta _{00}[q(k)]{\sqrt[{8}]{1-k^{2}}}}
ϑ
00
[
q
(
k
)
2
]
=
ϑ
00
[
q
(
k
)
]
cos
[
1
2
arcsin
(
k
)
]
{\displaystyle \vartheta _{00}[q(k)^{2}]=\vartheta _{00}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}
Verallgemeinert können die Nomenpotenzierungstheoreme mit der jacobischen Amplitudenfunktion so erzeugt werden:
ϑ
00
[
q
(
k
)
3
]
=
ϑ
00
[
q
(
k
)
]
sn
[
2
3
K
(
k
)
;
k
]
3
cd
[
2
3
K
(
k
)
;
k
]
{\displaystyle \vartheta _{00}[q(k)^{3}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{3}}K(k);k]}{{\sqrt {3}}\,{\text{cd}}[{\tfrac {2}{3}}K(k);k]}}}
ϑ
00
[
q
(
k
)
5
]
=
ϑ
00
[
q
(
k
)
]
sn
[
2
5
K
(
k
)
;
k
]
sn
[
4
5
K
(
k
)
;
k
]
5
cd
[
2
5
K
(
k
)
;
k
]
cd
[
4
5
K
(
k
)
;
k
]
{\displaystyle \vartheta _{00}[q(k)^{5}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{5}}K(k);k]\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]}{{\sqrt {5}}\,{\text{cd}}[{\tfrac {2}{5}}K(k);k]\,{\text{cd}}[{\tfrac {4}{5}}K(k);k]}}}
ϑ
00
[
q
(
k
)
7
]
=
ϑ
00
[
q
(
k
)
]
sn
[
2
7
K
(
k
)
;
k
]
sn
[
4
7
K
(
k
)
;
k
]
sn
[
6
7
K
(
k
)
;
k
]
7
cd
[
2
7
K
(
k
)
;
k
]
cd
[
4
7
K
(
k
)
;
k
]
cd
[
6
7
K
(
k
)
;
k
]
{\displaystyle \vartheta _{00}[q(k)^{7}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{7}}K(k);k]\,{\text{sn}}[{\tfrac {4}{7}}K(k);k]\,{\text{sn}}[{\tfrac {6}{7}}K(k);k]}{{\sqrt {7}}\,{\text{cd}}[{\tfrac {2}{7}}K(k);k]\,{\text{cd}}[{\tfrac {4}{7}}K(k);k]\,{\text{cd}}[{\tfrac {6}{7}}K(k);k]}}}
Die Abkürzung sn steht für den Sinus Amplitudinis und die Abkürzung cd stellt den Quotienten des Cosinus amplitudinis dividiert durch das Delta amplitudinis dar. Außerdem gilt für die Nomenkubizierung folgendes Theorem:
ϑ
01
⟨
q
{
tan
[
1
2
arctan
(
t
3
)
]
}
3
⟩
=
ϑ
01
⟨
q
{
tan
[
1
2
arctan
(
t
3
)
]
}
⟩
3
−
1
/
2
(
2
t
4
−
t
2
+
1
−
t
2
+
2
+
t
2
+
1
)
1
/
2
{\displaystyle \vartheta _{01}{\bigl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}^{3}{\bigr \rangle }=\vartheta _{01}{\bigl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}{\bigr \rangle }\,3^{-1/2}\,{\bigl (}{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}{\bigr )}^{1/2}}
Und für die Quintierung gilt folgendes Rechenverfahren:
ϑ
01
[
q
(
ε
)
5
]
=
ϑ
01
[
q
(
ε
)
]
5
−
1
/
2
2
w
R
5
(
ε
)
+
1
{\displaystyle \vartheta _{01}{\bigl [}q(\varepsilon )^{5}{\bigr ]}=\vartheta _{01}{\bigl [}q(\varepsilon ){\bigr ]}5^{-1/2}{\sqrt {2\,w_{R5}(\varepsilon )+1}}}
ϑ
00
[
q
(
ε
)
5
]
=
ϑ
00
[
q
(
ε
)
]
5
−
1
/
2
2
W
R
5
(
ε
)
+
1
{\displaystyle \vartheta _{00}{\bigl [}q(\varepsilon )^{5}{\bigr ]}=\vartheta _{00}{\bigl [}q(\varepsilon ){\bigr ]}5^{-1/2}{\sqrt {2\,W_{R5}(\varepsilon )+1}}}
Dabei soll die kleine reduzierte webersche Modulfunktion
w
R
5
(
ε
)
{\displaystyle w_{R5}(\varepsilon )}
w
R
5
(
ε
)
=
2
[
q
(
ε
)
5
;
q
(
ε
)
10
]
∞
[
q
(
ε
)
;
q
(
ε
)
2
]
∞
5
=
nc
[
4
5
K
(
ε
)
;
ε
]
−
nc
[
2
5
K
(
ε
)
;
ε
]
{\displaystyle w_{R5}(\varepsilon )={\frac {2\,[q(\varepsilon )^{5};q(\varepsilon )^{10}]_{\infty }}{[q(\varepsilon );q(\varepsilon )^{2}]_{\infty }^{5}}}={\text{nc}}{\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}-{\text{nc}}{\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}}
w
R
5
(
ε
)
6
−
2
w
R
5
(
ε
)
5
=
tan
[
2
arctan
(
ε
)
]
2
[
2
w
R
5
(
ε
)
+
1
]
{\displaystyle w_{R5}(\varepsilon )^{6}-2\,w_{R5}(\varepsilon )^{5}=\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigl [}2\,w_{R5}(\varepsilon )+1{\bigr ]}}
Und die große reduzierte webersche Modulfunktion
W
R
5
(
ε
)
{\displaystyle W_{R5}(\varepsilon )}
W
R
5
(
ε
)
=
2
w
R
5
(
ε
)
−
1
w
R
5
[
ε
2
(
1
+
1
−
ε
2
)
−
2
]
=
dn
[
2
5
K
(
ε
)
;
ε
]
+
dn
[
4
5
K
(
ε
)
;
ε
]
{\displaystyle W_{R5}(\varepsilon )=2\,w_{R5}(\varepsilon )^{-1}\,w_{R5}[\varepsilon ^{2}(1+{\sqrt {1-\varepsilon ^{2}}})^{-2}]={\text{dn}}{\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}+{\text{dn}}{\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}}
2
W
R
5
(
ε
)
5
−
W
R
5
(
ε
)
6
=
sin
[
2
arcsin
(
ε
)
]
2
[
2
W
R
5
(
ε
)
+
1
]
{\displaystyle 2\,W_{R5}(\varepsilon )^{5}-W_{R5}(\varepsilon )^{6}=\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigl [}2\,W_{R5}(\varepsilon )+1{\bigr ]}}
Rechenbeispiele für das Kubizierungstheorem:
Erstes Beispiel:
t
=
3
2
−
1
2
5
{\displaystyle {\color {blueviolet}t={\tfrac {3}{2}}-{\tfrac {1}{2}}{\sqrt {5}}}}
q
⟨
tan
{
1
2
arctan
[
(
3
2
−
1
2
5
)
3
]
}
⟩
=
exp
(
−
10
π
)
{\displaystyle q{\bigl \langle }\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}({\color {blueviolet}{\tfrac {3}{2}}-{\tfrac {1}{2}}{\sqrt {5}}})^{3}{\bigr ]}{\bigr \}}{\bigr \rangle }={\color {blue}\exp(-{\sqrt {10}}\,\pi )}}
ϑ
01
[
exp
(
−
3
10
π
)
]
=
ϑ
01
[
exp
(
−
10
π
)
]
6
−
1
/
2
[
(
3
−
5
)
(
6
+
5
)
(
3
+
6
)
+
15
−
3
]
1
/
2
{\displaystyle {\color {ForestGreen}\vartheta _{01}[{\color {Navy}\exp(-3{\sqrt {10}}\,\pi )}]=\vartheta _{01}[{\color {blue}\exp(-{\sqrt {10}}\,\pi )}]\,6^{-1/2}\,{\bigl [}(3-{\sqrt {5}}){\sqrt {({\sqrt {6}}+{\sqrt {5}})(3+{\sqrt {6}})}}+{\sqrt {15}}-{\sqrt {3}}{\bigr ]}^{1/2}}}
Zweites Beispiel:
t
=
2
+
1
2
−
1
2
4
2
+
5
{\displaystyle {\color {blueviolet}t={\sqrt {2}}+{\tfrac {1}{2}}-{\tfrac {1}{2}}{\sqrt {4{\sqrt {2}}+5}}}}
q
⟨
tan
{
1
2
arctan
[
(
2
+
1
2
−
1
2
4
2
+
5
)
3
]
}
⟩
=
exp
(
−
14
π
)
{\displaystyle q{\bigl \langle }\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\bigl (}{\color {blueviolet}{\sqrt {2}}+{\tfrac {1}{2}}-{\tfrac {1}{2}}{\sqrt {4{\sqrt {2}}+5}}}{\bigr )}^{3}{\bigr ]}{\bigr \}}{\bigr \rangle }={\color {blue}\exp(-{\sqrt {14}}\,\pi )}}
ϑ
01
[
exp
(
−
3
14
π
)
]
=
ϑ
01
[
exp
(
−
14
π
)
]
6
−
1
/
2
(
12
2
+
15
+
8
2
+
11
−
7
−
3
)
1
/
2
{\displaystyle {\color {ForestGreen}\vartheta _{01}[{\color {Navy}\exp(-3{\sqrt {14}}\,\pi )}]=\vartheta _{01}[{\color {blue}\exp(-{\sqrt {14}}\,\pi )}]\,6^{-1/2}\,{\bigl (}{\sqrt {12{\sqrt {2}}+15}}+{\sqrt {8{\sqrt {2}}+11}}-{\sqrt {7}}-{\sqrt {3}}{\bigr )}^{1/2}}}
Zu den Transformationen des Elliptischen Nomens bei den Nicht-Nullwertfunktionen dienen jene Formeln:
ϑ
00
(
x
;
c
2
)
=
ϑ
00
(
c
)
−
1
/
2
ϑ
01
(
c
)
−
1
/
2
ϑ
00
(
1
2
x
+
1
4
π
;
c
)
ϑ
00
(
1
2
x
−
1
4
π
;
c
)
{\displaystyle \vartheta _{00}(x;c^{2})=\vartheta _{00}(c)^{-1/2}\vartheta _{01}(c)^{-1/2}\vartheta _{00}({\tfrac {1}{2}}x+{\tfrac {1}{4}}\pi ;c)\vartheta _{00}({\tfrac {1}{2}}x-{\tfrac {1}{4}}\pi ;c)}
ϑ
01
(
x
;
c
2
)
=
ϑ
00
(
c
)
−
1
/
2
ϑ
01
(
c
)
−
1
/
2
ϑ
00
(
1
2
x
;
c
)
ϑ
01
(
1
2
x
;
c
)
{\displaystyle \vartheta _{01}(x;c^{2})=\vartheta _{00}(c)^{-1/2}\vartheta _{01}(c)^{-1/2}\vartheta _{00}({\tfrac {1}{2}}x;c)\vartheta _{01}({\tfrac {1}{2}}x;c)}
ϑ
00
(
x
;
c
1
/
2
)
=
[
ϑ
00
(
c
)
2
+
ϑ
10
(
c
)
2
]
−
1
/
2
[
ϑ
00
(
x
;
c
)
2
+
ϑ
10
(
x
;
c
)
2
]
{\displaystyle \vartheta _{00}(x;c^{1/2})=[\vartheta _{00}(c)^{2}+\vartheta _{10}(c)^{2}]^{-1/2}[\vartheta _{00}(x;c)^{2}+\vartheta _{10}(x;c)^{2}]}
ϑ
01
(
x
;
c
1
/
2
)
=
[
ϑ
00
(
c
)
2
−
ϑ
10
(
c
)
2
]
−
1
/
2
[
ϑ
00
(
x
;
c
)
2
−
ϑ
10
(
x
;
c
)
2
]
{\displaystyle \vartheta _{01}(x;c^{1/2})=[\vartheta _{00}(c)^{2}-\vartheta _{10}(c)^{2}]^{-1/2}[\vartheta _{00}(x;c)^{2}-\vartheta _{10}(x;c)^{2}]}
ϑ
10
(
x
;
c
1
/
2
)
=
2
1
/
2
ϑ
10
(
c
)
−
1
/
2
ϑ
00
(
c
)
−
1
/
2
ϑ
10
(
x
;
c
)
ϑ
00
(
x
;
c
)
{\displaystyle \vartheta _{10}(x;c^{1/2})=2^{1/2}\vartheta _{10}(c)^{-1/2}\vartheta _{00}(c)^{-1/2}\vartheta _{10}(x;c)\vartheta _{00}(x;c)}
Die Formeln für die Quadrierung des Nomens sollen mit Hilfe der Definitionen nach Whittaker und Watson gezeigt werden:
ϑ
00
(
1
2
x
;
c
)
=
∏
n
=
1
∞
(
1
−
c
2
n
)
[
1
+
2
cos
(
x
)
c
2
n
−
1
+
c
4
n
−
2
]
{\displaystyle \vartheta _{00}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})[1+2\cos(x)c^{2n-1}+c^{4n-2}]}
ϑ
01
(
1
2
x
;
c
)
=
∏
n
=
1
∞
(
1
−
c
2
n
)
[
1
−
2
cos
(
x
)
c
2
n
−
1
+
c
4
n
−
2
]
{\displaystyle \vartheta _{01}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})[1-2\cos(x)c^{2n-1}+c^{4n-2}]}
Diese beiden Definitionsformeln werden miteinander multipliziert:
ϑ
00
(
1
2
x
;
c
)
ϑ
00
(
1
2
x
;
c
)
=
∏
n
=
1
∞
(
1
−
c
2
n
)
2
[
1
+
2
cos
(
x
)
c
2
n
−
1
+
c
4
n
−
2
]
[
1
−
2
cos
(
x
)
c
2
n
−
1
+
c
4
n
−
2
]
=
{\displaystyle \vartheta _{00}({\tfrac {1}{2}}x;c)\,\vartheta _{00}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})^{2}[1+2\cos(x)c^{2n-1}+c^{4n-2}][1-2\cos(x)c^{2n-1}+c^{4n-2}]=}
=
∏
n
=
1
∞
(
1
−
c
2
n
)
2
{
1
−
2
[
2
cos
(
x
)
2
−
1
]
c
4
n
−
2
+
c
8
n
−
4
}
=
∏
n
=
1
∞
(
1
−
c
2
n
)
2
[
1
−
2
cos
(
2
x
)
c
4
n
−
2
+
c
8
n
−
4
]
=
{\displaystyle =\prod _{n=1}^{\infty }(1-c^{2n})^{2}\{1-2[2\cos(x)^{2}-1]c^{4n-2}+c^{8n-4}\}=\prod _{n=1}^{\infty }(1-c^{2n})^{2}[1-2\cos(2x)c^{4n-2}+c^{8n-4}]=}
=
[
∏
n
=
1
∞
1
−
c
2
n
1
+
c
2
n
]
{
∏
n
=
1
∞
(
1
−
c
4
n
)
[
1
−
2
cos
(
2
x
)
c
4
n
−
2
+
c
8
n
−
4
]
}
=
[
∏
n
=
1
∞
1
−
c
2
n
1
+
c
2
n
]
ϑ
01
(
x
,
c
2
)
=
{\displaystyle ={\biggl [}\prod _{n=1}^{\infty }{\frac {1-c^{2n}}{1+c^{2n}}}{\biggr ]}{\biggl \{}\prod _{n=1}^{\infty }(1-c^{4n}){\bigl [}1-2\cos(2x)c^{4n-2}+c^{8n-4}{\bigr ]}{\biggr \}}={\biggl [}\prod _{n=1}^{\infty }{\frac {1-c^{2n}}{1+c^{2n}}}{\biggr ]}\vartheta _{01}(x,c^{2})=}
=
ϑ
01
(
c
2
)
ϑ
01
(
x
,
c
2
)
=
ϑ
00
(
c
)
1
/
2
ϑ
01
(
c
)
1
/
2
ϑ
01
(
x
,
c
2
)
{\displaystyle =\vartheta _{01}(c^{2})\vartheta _{01}(x,c^{2})=\vartheta _{00}(c)^{1/2}\vartheta _{01}(c)^{1/2}\vartheta _{01}(x,c^{2})}
Wenn der linke Eintrag in der Klammer der Thetafunktion einen Wert des Musters π·t mit t ∈ ℚ annimmt, dann können alle Werte der Funktionen ϑ₀₀, ϑ₀₁ und ϑ₁₀ mit dem hier abgebildeten elliptischen Nomen mit den Jacobifunktionen sn, cn und dn ausgedrückt werden:
q
(
k
)
=
exp
[
−
π
K
(
1
−
k
2
)
K
(
k
)
−
1
]
{\displaystyle q(k)=\exp[-\pi K({\sqrt {1-k^{2}}})K(k)^{-1}]}
Für alle
0
<
k
<
1
{\displaystyle 0<k<1}
ϑ
00
[
0
;
q
(
k
)
]
=
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[0;q(k)]={\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
2
π
;
q
(
k
)
]
=
1
−
k
2
4
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{2}}\pi ;q(k)]={\sqrt[{4}]{1-k^{2}}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
4
π
;
q
(
k
)
]
=
1
2
8
4
1
−
k
2
16
1
+
1
−
k
2
4
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{4}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{8}}{\sqrt[{16}]{1-k^{2}}}{\sqrt[{4}]{1+{\sqrt {1-k^{2}}}}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
6
π
;
q
(
k
)
]
=
1
2
1
−
k
2
12
4
dn
[
1
3
K
(
k
)
;
k
]
nc
[
2
3
K
(
k
)
;
k
]
3
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{6}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{12}]{1-k^{2}}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {1}{3}}K(k);k]\operatorname {nc} [{\tfrac {2}{3}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
3
π
;
q
(
k
)
]
=
1
2
4
dn
[
2
3
K
(
k
)
;
k
]
dc
[
2
3
K
(
k
)
;
k
]
3
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{3}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {2}{3}}K(k);k]\operatorname {dc} [{\tfrac {2}{3}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
10
π
;
q
(
k
)
]
=
1
2
1
−
k
2
4
8
w
R
5
(
k
)
sn
[
2
5
K
(
k
)
;
k
]
ns
[
4
5
K
(
k
)
;
k
]
nc
[
4
5
K
(
k
)
;
k
]
nd
[
4
5
K
(
k
)
;
k
]
5
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{10}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {nd} [{\tfrac {4}{5}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
1
5
π
;
q
(
k
)
]
=
1
2
8
w
R
5
(
k
)
sn
[
4
5
K
(
k
)
;
k
]
ns
[
2
5
K
(
k
)
;
k
]
nc
[
2
5
K
(
k
)
;
k
]
dn
[
2
5
K
(
k
)
;
k
]
4
5
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {1}{5}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {dn} [{\tfrac {2}{5}}K(k);k]^{4}}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
3
10
π
;
q
(
k
)
]
=
1
2
1
−
k
2
4
8
w
R
5
(
k
)
sn
[
4
5
K
(
k
)
;
k
]
ns
[
2
5
K
(
k
)
;
k
]
nc
[
2
5
K
(
k
)
;
k
]
nd
[
2
5
K
(
k
)
;
k
]
5
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {3}{10}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {nd} [{\tfrac {2}{5}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}
ϑ
00
[
2
5
π
;
q
(
k
)
]
=
1
2
8
w
R
5
(
k
)
sn
[
2
5
K
(
k
)
;
k
]
ns
[
4
5
K
(
k
)
;
k
]
nc
[
4
5
K
(
k
)
;
k
]
dn
[
4
5
K
(
k
)
;
k
]
4
5
2
π
−
1
K
(
k
)
{\displaystyle \vartheta _{00}[{\tfrac {2}{5}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {dn} [{\tfrac {4}{5}}K(k);k]^{4}}}{\sqrt {2\pi ^{-1}K(k)}}}
Zur Ermittlung der Werte von ϑ₀₁ aus den Werten von ϑ₀₀ dient diese Symmetriebeziehung:
ϑ
01
(
x
;
c
)
=
ϑ
00
(
1
2
π
−
x
;
c
)
{\displaystyle \vartheta _{01}(x;c)=\vartheta _{00}({\tfrac {1}{2}}\pi -x;c)}
Zur Ermittlung der Werte von ϑ₁₀ gereichen jene Theoreme:
ϑ
10
(
x
;
c
)
4
=
ϑ
00
(
c
)
3
ϑ
00
(
2
x
;
c
)
−
ϑ
01
(
x
;
c
)
4
{\displaystyle \vartheta _{10}(x;c)^{4}=\vartheta _{00}(c)^{3}\vartheta _{00}(2x;c)-\vartheta _{01}(x;c)^{4}}
ϑ
10
(
x
;
c
)
4
=
ϑ
00
(
x
;
c
)
4
−
ϑ
01
(
c
)
3
ϑ
01
(
2
x
;
c
)
{\displaystyle \vartheta _{10}(x;c)^{4}=\vartheta _{00}(x;c)^{4}-\vartheta _{01}(c)^{3}\vartheta _{01}(2x;c)}
Diese Werte entstehen durch Einsatz von
k
=
λ
∗
(
1
)
=
1
2
2
:
{\displaystyle k=\lambda ^{*}(1)={\tfrac {1}{2}}{\sqrt {2}}\colon }
ϑ
00
(
1
2
π
;
e
−
π
)
=
G
{\displaystyle \vartheta _{00}({\tfrac {1}{2}}\pi ;{\text{e}}^{-\pi })={\sqrt {G}}}
ϑ
00
(
1
4
π
;
e
−
π
)
=
2
−
3
/
16
2
+
1
4
G
{\displaystyle \vartheta _{00}({\tfrac {1}{4}}\pi ;{\text{e}}^{-\pi })=2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt {G}}}
ϑ
00
(
1
3
π
;
e
−
π
)
=
2
−
1
/
4
2
+
3
6
G
{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{6}]{2+{\sqrt {3}}}}{\sqrt {G}}}
ϑ
00
(
1
5
π
;
e
−
π
)
=
2
−
1
/
4
2
(
5
+
2
)
cos
(
1
20
π
)
tan
(
3
20
π
)
5
G
{\displaystyle \vartheta _{00}({\tfrac {1}{5}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{5}]{2({\sqrt {5}}+2)\cos({\tfrac {1}{20}}\pi )\tan({\tfrac {3}{20}}\pi )}}{\sqrt {G}}}
ϑ
00
(
2
5
π
;
e
−
π
)
=
2
−
1
/
4
2
(
5
+
2
)
sin
(
1
20
π
)
cot
(
3
20
π
)
5
G
{\displaystyle \vartheta _{00}({\tfrac {2}{5}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{5}]{2({\sqrt {5}}+2)\sin({\tfrac {1}{20}}\pi )\cot({\tfrac {3}{20}}\pi )}}{\sqrt {G}}}
Auch hier steht
G
{\displaystyle G}
G
=
2
π
−
1
K
(
1
2
2
)
{\displaystyle G={\sqrt {2}}\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}
Diese Werte entstehen durch Einsatz von
k
=
λ
∗
(
2
)
=
2
−
1
:
{\displaystyle k=\lambda ^{*}(2)={\sqrt {2}}-1\colon }
ϑ
00
(
1
2
π
;
e
−
2
π
)
=
2
−
5
/
8
2
+
1
4
π
−
1
/
2
β
(
3
8
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{2}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-5/8}{\sqrt[{4}]{{\sqrt {2}}+1}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}
ϑ
00
(
1
6
π
;
e
−
2
π
)
=
2
−
9
/
8
2
+
1
4
3
+
2
3
π
−
1
/
2
β
(
3
8
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{6}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-9/8}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt[{3}]{{\sqrt {3}}+{\sqrt {2}}}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}
ϑ
00
(
1
3
π
;
e
−
2
π
)
=
2
−
1
/
8
sin
(
5
24
π
)
3
+
2
3
π
−
1
/
2
β
(
3
8
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-1/8}\sin({\tfrac {5}{24}}\pi ){\sqrt[{3}]{{\sqrt {3}}+{\sqrt {2}}}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}
Und jene Werte[ 29]
k
=
λ
∗
(
5
)
=
sin
[
1
2
arcsin
(
5
−
2
)
]
:
{\displaystyle k=\lambda ^{*}(5)=\sin[{\tfrac {1}{2}}\arcsin({\sqrt {5}}-2)]\colon }
ϑ
00
(
1
2
π
;
e
−
5
π
)
=
2
−
47
/
40
5
−
5
/
16
(
5
−
1
)
5
/
8
(
5
+
2
+
1
)
cos
(
1
20
π
)
1
/
2
π
−
1
/
2
β
(
9
20
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{2}}\pi ;{\text{e}}^{-{\sqrt {5}}\pi })=2^{-47/40}5^{-5/16}({\sqrt {5}}-1)^{5/8}({\sqrt {{\sqrt {5}}+2}}+1)\cos({\tfrac {1}{20}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {9}{20}})^{1/2}}
ϑ
00
(
1
6
π
;
e
−
5
π
)
=
2
−
47
/
40
5
−
5
/
16
(
2
5
−
2
3
+
1
+
1
)
5
−
1
8
4
+
15
6
cos
(
1
20
π
)
1
/
2
π
−
1
/
2
β
(
9
20
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{6}}\pi ;{\text{e}}^{-{\sqrt {5}}\pi })=2^{-47/40}5^{-5/16}({\sqrt {2{\sqrt {5}}-2{\sqrt {3}}+1}}+1){\sqrt[{8}]{{\sqrt {5}}-1}}{\sqrt[{6}]{4+{\sqrt {15}}}}\cos({\tfrac {1}{20}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {9}{20}})^{1/2}}
ϑ
00
(
1
3
π
;
e
−
5
π
)
=
2
−
37
/
40
5
−
5
/
16
(
5
+
1
)
5
/
8
4
+
15
6
cos
(
1
20
π
)
1
/
2
π
−
1
/
2
β
(
9
20
)
1
/
2
{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-{\sqrt {5}}\pi })=2^{-37/40}5^{-5/16}({\sqrt {5}}+1)^{5/8}{\sqrt[{6}]{4+{\sqrt {15}}}}\cos({\tfrac {1}{20}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {9}{20}})^{1/2}}
Für die Funktionen ϑ₀₀, ϑ₀₁ und ϑ₁₀ gelten diese Symmetriebeziehungen:
ϑ
00
(
x
;
c
)
=
ϑ
00
(
−
x
;
c
)
=
ϑ
00
(
x
+
π
;
c
)
{\displaystyle \vartheta _{00}(x;c)=\vartheta _{00}(-x;c)=\vartheta _{00}(x+\pi ;c)}
ϑ
01
(
x
;
c
)
=
ϑ
01
(
−
x
;
c
)
=
ϑ
01
(
x
+
π
;
c
)
{\displaystyle \vartheta _{01}(x;c)=\vartheta _{01}(-x;c)=\vartheta _{01}(x+\pi ;c)}
ϑ
10
(
x
;
c
)
=
ϑ
10
(
−
x
;
c
)
=
−
ϑ
10
(
x
+
π
;
c
)
{\displaystyle \vartheta _{10}(x;c)=\vartheta _{10}(-x;c)=-\vartheta _{10}(x+\pi ;c)}
Der Allgemeinfall der Theta-Nicht-Nullwertfunktionen ϑ₀₀[x;q(k)], ϑ₀₁[x;q(k)] und ϑ₁₀[x;q(k)] kann weder mit den Jacobi-Funktionen sn, cn und dn noch mit den Theta-Nullwertfunktionen noch mit den Kombinationen beider zuletzt genannten Funktionsklassen ausgedrückt werden. Jedoch können sowohl die Jacobi-Funktionen als auch die Theta-Nullwertfunktionen sehr wohl alleine durch den Allgemeinfall der Theta-Nicht-Nullwertfunktionen dargestellt werden. Basierend auf diesen Tatsachen bilden die Thetafunktionen zusammen mit den elliptischen Integralen die Grundlage für alle elliptischen Jacobi-Funktionen und Modulfunktionen.
Carl Gustav Jacobi Adrien-Marie Legendre Die partiellen Ableitungen der Theta-Nicht-Nullwertfunktionen nach dem linken Klammereintrag lauten[ 30] [ 31]
ϑ
01
′
(
v
;
w
)
=
∂
∂
v
ϑ
01
(
v
;
w
)
=
[
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
]
ϑ
01
(
v
;
w
)
zn
{
v
2
[
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
]
;
ϑ
00
(
w
)
2
−
ϑ
01
(
w
)
2
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
}
+
{\displaystyle \vartheta _{01}'(v;w)={\frac {\partial }{\partial v}}\vartheta _{01}(v;w)={\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]}\vartheta _{01}(v;w)\,{\text{zn}}{\biggl \{}{\frac {v}{2}}{\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]};{\frac {\vartheta _{00}(w)^{2}-\vartheta _{01}(w)^{2}}{\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}}}{\biggr \}}+}
+
1
2
ϑ
00
(
w
)
ϑ
01
(
w
)
2
ϑ
01
(
1
4
π
;
w
)
2
ϑ
01
(
1
4
π
+
v
;
w
)
2
−
ϑ
01
(
1
4
π
−
v
;
w
)
2
ϑ
00
(
1
2
v
;
w
)
2
ϑ
01
(
1
2
v
;
w
)
2
{\displaystyle +{\frac {1}{2}}\vartheta _{00}(w)\vartheta _{01}(w)^{2}\vartheta _{01}({\tfrac {1}{4}}\pi ;w)^{2}{\frac {\vartheta _{01}({\tfrac {1}{4}}\pi +v;w)^{2}-\vartheta _{01}({\tfrac {1}{4}}\pi -v;w)^{2}}{\vartheta _{00}({\tfrac {1}{2}}v;w)^{2}\vartheta _{01}({\tfrac {1}{2}}v;w)^{2}}}}
ϑ
00
′
(
v
;
w
)
=
∂
∂
v
ϑ
00
(
v
;
w
)
=
[
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
]
ϑ
00
(
v
;
w
)
zn
{
v
2
[
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
]
;
ϑ
00
(
w
)
2
−
ϑ
01
(
w
)
2
ϑ
00
(
w
)
2
+
ϑ
01
(
w
)
2
}
−
{\displaystyle \vartheta _{00}'(v;w)={\frac {\partial }{\partial v}}\vartheta _{00}(v;w)={\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]}\vartheta _{00}(v;w)\,{\text{zn}}{\biggl \{}{\frac {v}{2}}{\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]};{\frac {\vartheta _{00}(w)^{2}-\vartheta _{01}(w)^{2}}{\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}}}{\biggr \}}-}
−
1
2
ϑ
01
(
w
)
ϑ
00
(
w
)
2
ϑ
00
(
1
4
π
;
w
)
2
ϑ
00
(
1
4
π
−
v
;
w
)
2
−
ϑ
00
(
1
4
π
+
v
;
w
)
2
ϑ
00
(
1
2
v
;
w
)
2
ϑ
01
(
1
2
v
;
w
)
2
{\displaystyle -{\frac {1}{2}}\vartheta _{01}(w)\vartheta _{00}(w)^{2}\vartheta _{00}({\tfrac {1}{4}}\pi ;w)^{2}{\frac {\vartheta _{00}({\tfrac {1}{4}}\pi -v;w)^{2}-\vartheta _{00}({\tfrac {1}{4}}\pi +v;w)^{2}}{\vartheta _{00}({\tfrac {1}{2}}v;w)^{2}\vartheta _{01}({\tfrac {1}{2}}v;w)^{2}}}}
Für diese Theta-Ableitungsfunktionen in der so definierten Form etablierte sich die Bezeichnung „Elliptic Theta Prime“ im englischen Sprachraum. Durch den Zusatz der elliptischen Nomenfunktion im rechten Klammereintrag können die Ableitungen so formuliert werden:
∂
∂
x
ϑ
01
[
x
;
q
(
k
)
]
=
2
π
−
1
K
(
k
)
ϑ
01
[
x
;
q
(
k
)
]
zn
[
2
π
−
1
K
(
k
)
x
;
k
]
{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{01}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{01}[x;q(k)]{\text{zn}}[2\pi ^{-1}K(k)x;k]}
∂
∂
x
ϑ
00
[
x
;
q
(
k
)
]
=
2
π
−
1
K
(
k
)
ϑ
00
[
x
;
q
(
k
)
]
{
zn
[
2
π
−
1
K
(
k
)
x
;
k
]
−
k
2
sn
[
2
π
−
1
K
(
k
)
x
;
k
]
cd
[
2
π
−
1
K
(
k
)
x
;
k
]
}
{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{00}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{00}[x;q(k)]\{{\text{zn}}[2\pi ^{-1}K(k)x;k]-k^{2}{\text{sn}}[2\pi ^{-1}K(k)x;k]{\text{cd}}[2\pi ^{-1}K(k)x;k]\}}
∂
∂
x
ϑ
10
[
x
;
q
(
k
)
]
=
2
π
−
1
K
(
k
)
ϑ
10
[
x
;
q
(
k
)
]
{
zn
[
2
π
−
1
K
(
k
)
x
;
k
]
−
sn
[
2
π
−
1
K
(
k
)
x
;
k
]
dc
[
2
π
−
1
K
(
k
)
x
;
k
]
}
{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{10}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{10}[x;q(k)]\{{\text{zn}}[2\pi ^{-1}K(k)x;k]-{\text{sn}}[2\pi ^{-1}K(k)x;k]{\text{dc}}[2\pi ^{-1}K(k)x;k]\}}
Mit dem Kürzel zn wird die jacobische Zetafunktion beziehungsweise das Zeta amplitudinis dargestellt:
zn
(
z
;
k
)
=
E
[
am
(
z
;
k
)
;
k
]
−
E
(
k
)
K
(
k
)
−
1
z
{\displaystyle {\text{zn}}(z;k)=E[{\text{am}}(z;k);k]-E(k)K(k)^{-1}z}
Hierbei ist E(ε) das vollständige elliptische Integral zweiter Art:
E
(
ε
)
=
∫
0
π
/
2
1
−
ε
2
sin
(
φ
)
2
d
φ
=
2
∫
0
1
(
y
2
+
1
)
2
−
4
ε
2
y
2
(
y
2
+
1
)
2
d
y
{\displaystyle E(\varepsilon )=\int _{0}^{\pi /2}{\sqrt {1-{\varepsilon }^{2}\sin(\varphi )^{2}}}\mathrm {d} \varphi =2\int _{0}^{1}{\frac {\sqrt {(y^{2}+1)^{2}-4{\varepsilon }^{2}y^{2}}}{(y^{2}+1)^{2}}}\mathrm {d} y}
Und E(α;ε) ist das unvollständige elliptische Integral zweiter Art:
E
(
α
;
ε
)
=
∫
0
1
α
1
−
ε
2
sin
(
α
φ
)
2
∂
φ
{\displaystyle E(\alpha ;\varepsilon )=\int _{0}^{1}\alpha {\sqrt {1-{\varepsilon }^{2}\sin(\alpha \varphi )^{2}}}\,\partial \varphi }
Dieses Integral E(ε) nennt das Verhältnis des Viertelumfangs zur größeren Halbachse bei der Ellipse mit dem Wert ε als spezifische Exzentrizität. Diese Definition und die zugehörige Klassifizierung wurden insbesondere durch den Mathematiker Adrien-Marie Legendre aufgestellt.
Als Lösungen der Wärmeleitungsgleichung erfüllen die Thetafunktionen diese Differentialgleichungen:
∂
2
∂
v
2
ϑ
10
(
v
;
w
)
=
−
4
w
∂
∂
w
ϑ
10
(
v
;
w
)
{\displaystyle {\frac {\partial ^{2}}{\partial v^{2}}}\vartheta _{10}(v;w)=-4w{\frac {\partial }{\partial w}}\vartheta _{10}(v;w)}
∂
2
∂
v
2
ϑ
00
(
v
;
w
)
=
−
4
w
∂
∂
w
ϑ
00
(
v
;
w
)
{\displaystyle {\frac {\partial ^{2}}{\partial v^{2}}}\vartheta _{00}(v;w)=-4w{\frac {\partial }{\partial w}}\vartheta _{00}(v;w)}
∂
2
∂
v
2
ϑ
01
(
v
;
w
)
=
−
4
w
∂
∂
w
ϑ
01
(
v
;
w
)
{\displaystyle {\frac {\partial ^{2}}{\partial v^{2}}}\vartheta _{01}(v;w)=-4w{\frac {\partial }{\partial w}}\vartheta _{01}(v;w)}
Die Thetafunktion spielt eine wichtige Rolle[ 32] Wärmeleitung und der Diffusion , für reelle
x
{\displaystyle x}
t
>
0
{\displaystyle t>0}
partiellen Differentialgleichung :
∂
∂
t
ϑ
(
x
,
i
t
)
=
1
4
π
∂
2
∂
x
2
ϑ
(
x
,
i
t
)
,
{\displaystyle {\frac {\partial }{\partial t}}\vartheta (x,it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x,it),}
Dies ist durch das Einsetzen von folgender Formel ersichtlich:
ϑ
(
x
,
i
t
)
=
∑
n
=
−
∞
∞
e
−
n
2
⋅
π
⋅
t
+
2
π
i
n
x
=
1
+
2
∑
n
=
1
∞
e
−
n
2
⋅
π
⋅
t
cos
(
2
π
n
x
)
{\displaystyle \vartheta (x,it)=\sum _{n=-\infty }^{\infty }e^{-n^{2}\cdot \pi \cdot t+2\pi inx}=1+2\sum _{n=1}^{\infty }e^{-n^{2}\cdot \pi \cdot t}\cos {(2\pi nx)}}
Der Formalismus entspricht einer Fourierentwicklung im Ortsraum mit Koeffizienten mit exponentiell abfallender Zeitabhängigkeit. Somit bildet die jacobische Thetafunktion den Wärmeleitungskern der eindimensionalen Wärmeleitungsgleichung[ 33]
Die Ableitungen der Theta-Nullwertfunktionen[ 34]
d
d
x
ϑ
10
(
x
)
=
1
2
π
x
ϑ
10
(
x
)
ϑ
00
(
x
)
2
E
[
ϑ
10
(
x
)
2
ϑ
00
(
x
)
2
]
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{10}(x)={\frac {1}{2\pi x}}\vartheta _{10}(x)\vartheta _{00}(x)^{2}E{\biggl [}{\frac {\vartheta _{10}(x)^{2}}{\vartheta _{00}(x)^{2}}}{\biggr ]}}
d
d
x
ϑ
00
(
x
)
=
ϑ
00
(
x
)
[
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
{
1
2
π
x
E
[
ϑ
00
(
x
)
2
−
ϑ
01
(
x
)
2
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
−
ϑ
01
(
x
)
2
4
x
}
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{00}(x)=\vartheta _{00}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{01}(x)^{2}}{4x}}{\biggr \}}}
d
d
x
ϑ
01
(
x
)
=
ϑ
01
(
x
)
[
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
{
1
2
π
x
E
[
ϑ
00
(
x
)
2
−
ϑ
01
(
x
)
2
ϑ
00
(
x
)
2
+
ϑ
01
(
x
)
2
]
−
ϑ
00
(
x
)
2
4
x
}
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{01}(x)=\vartheta _{01}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{00}(x)^{2}}{4x}}{\biggr \}}}
Und zueinander stehen die beiden zuletzt genannten Formeln somit in dieser Beziehung:
ϑ
01
(
x
)
[
d
d
x
ϑ
00
(
x
)
]
−
ϑ
00
(
x
)
[
d
d
x
ϑ
01
(
x
)
]
=
1
4
x
ϑ
00
(
x
)
ϑ
01
(
x
)
[
ϑ
00
(
x
)
4
−
ϑ
01
(
x
)
4
]
{\displaystyle \vartheta _{01}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{00}(x){\biggr ]}-\vartheta _{00}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{01}(x){\biggr ]}={\frac {1}{4x}}\,\vartheta _{00}(x)\,\vartheta _{01}(x){\bigl [}\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}{\bigr ]}}
Die Ableitungen der Quotienten aus jeweils zwei der drei hier genannten Thetafunktionen haben immer eine rationale Beziehung zu jenen drei Funktionen:
d
d
x
ϑ
10
(
x
)
ϑ
00
(
x
)
=
ϑ
10
(
x
)
ϑ
01
(
x
)
4
4
x
ϑ
00
(
x
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\vartheta _{10}(x)}{\vartheta _{00}(x)}}={\frac {\vartheta _{10}(x)\vartheta _{01}(x)^{4}}{4x\,\vartheta _{00}(x)}}}
d
d
x
ϑ
10
(
x
)
ϑ
01
(
x
)
=
ϑ
10
(
x
)
ϑ
00
(
x
)
4
4
x
ϑ
01
(
x
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\vartheta _{10}(x)}{\vartheta _{01}(x)}}={\frac {\vartheta _{10}(x)\vartheta _{00}(x)^{4}}{4x\,\vartheta _{01}(x)}}}
d
d
x
ϑ
00
(
x
)
ϑ
01
(
x
)
=
ϑ
00
(
x
)
5
−
ϑ
00
(
x
)
ϑ
01
(
x
)
4
4
x
ϑ
01
(
x
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\vartheta _{00}(x)}{\vartheta _{01}(x)}}={\frac {\vartheta _{00}(x)^{5}-\vartheta _{00}(x)\vartheta _{01}(x)^{4}}{4x\,\vartheta _{01}(x)}}}
Für die Herleitungen dieser Ableitungsformeln siehe die Artikel Elliptisches Nomen und Elliptische Lambda-Funktion !
Leonhard Euler Carl Friedrich Gauss Für die Theta-Nullwertfunktionen ϑ₀₀(x), ϑ₀₁(x) und ϑ₁₀(x) sind diese Integrale[ 35]
∫
0
1
ϑ
00
(
x
)
d
x
=
∑
k
=
−
∞
∞
1
k
2
+
1
=
π
coth
(
π
)
≈
3,153
348
{\displaystyle \int _{0}^{1}\vartheta _{00}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {1}{k^{2}+1}}=\pi \coth(\pi )\approx 3{,}153348}
∫
0
1
ϑ
01
(
x
)
d
x
=
∑
k
=
−
∞
∞
(
−
1
)
k
k
2
+
1
=
π
csch
(
π
)
≈
0,272
029
{\displaystyle \int _{0}^{1}\vartheta _{01}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k^{2}+1}}=\pi \,\operatorname {csch} (\pi )\approx 0{,}272029}
∫
0
1
ϑ
10
(
x
)
d
x
=
∑
k
=
−
∞
∞
4
(
2
k
+
1
)
2
+
4
=
π
tanh
(
π
)
≈
3,129
881
{\displaystyle \int _{0}^{1}\vartheta _{10}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {4}{(2k+1)^{2}+4}}=\pi \tanh(\pi )\approx 3{,}129881}
Die nun gezeigten Endresultate basieren auf den allgemeinen Cauchyschen Summenformeln.
Bernhard Riemann benutzte in seiner berühmten Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe Funktionalgleichung der Riemannschen Zetafunktion , es gilt nämlich folgende[ 36]
∫
0
∞
x
n
{
ϑ
00
[
exp
(
−
x
)
]
−
1
}
d
x
=
2
Γ
(
n
+
1
)
ζ
(
2
n
+
2
)
{\displaystyle \int _{0}^{\infty }x^{n}\{\vartheta _{00}[\exp(-x)]-1\}\,\mathrm {d} x=2\Gamma (n+1)\zeta (2n+2)}
Dieses Integral ist für alle Werte n > −½ gültig und konvergent.
Beispielsweise hat die Apéry-Konstante folgende Integraldarstellung:
ζ
(
3
)
=
π
−
1
/
2
∫
0
∞
x
{
ϑ
00
[
exp
(
−
x
)
]
−
1
}
d
x
{\displaystyle \zeta (3)=\pi ^{-1/2}\int _{0}^{\infty }{\sqrt {x}}\,\{\vartheta _{00}[\exp(-x)]-1\}\,\mathrm {d} x}
Aus dem genannten Zusammenhang zwischen Jacobischer Thetafunktion und Riemannscher Zetafunktion resultiert die nun folgende Formel:
γ
=
∫
0
∞
1
2
x
[
exp
(
x
2
)
erfc
(
x
)
+
2
π
−
1
/
2
x
−
1
]
{
ϑ
00
[
exp
(
−
x
2
)
]
−
1
}
d
x
{\displaystyle \gamma =\int _{0}^{\infty }{\frac {1}{2x}}[\exp(x^{2})\operatorname {erfc} (x)+2\pi ^{-1/2}x-1]\{\vartheta _{00}[\exp(-x^{2})]-1\}\,\mathrm {d} x}
Dabei wird mit γ die Euler-Mascheroni-Konstante und mit erfc(x) die komplementäre Gaußsche Fehlerfunktion dargestellt.
Diese Formel basiert auf folgender Summenreihe:
γ
=
∑
n
=
1
∞
[
ζ
(
2
n
)
2
n
−
ζ
(
2
n
+
1
)
2
n
+
1
]
{\displaystyle \gamma =\sum _{n=1}^{\infty }{\biggl [}{\frac {\zeta (2n)}{2n}}-{\frac {\zeta (2n+1)}{2n+1}}{\biggr ]}}
Erweitert kann für die Hurwitzsche Zetafunktion dieser Ausdruck formuliert werden:
∫
0
∞
x
n
{
ϑ
00
[
π
a
;
exp
(
−
x
)
]
−
1
}
d
x
=
Γ
(
n
+
1
)
ζ
(
2
n
+
2
)
/
ζ
(
−
2
n
−
1
)
[
ζ
(
−
2
n
−
1
;
a
)
+
ζ
(
−
2
n
−
1
;
1
−
a
)
]
{\displaystyle \int _{0}^{\infty }x^{n}\{\vartheta _{00}[\pi \,a;\exp(-x)]-1\}\,\mathrm {d} x=\Gamma (n+1)\zeta (2n+2)/\zeta (-2n-1){\bigl [}\zeta (-2n-1;a)+\zeta (-2n-1;1-a){\bigr ]}}
Für alle Zahlenpaare a und n mit den Kriterien
a
∈
C
∖
Z
{\displaystyle a\in \mathbb {C} \,\setminus \,\mathbb {Z} }
[
n
∈
C
∖
(
−
1
2
+
m
)
(
m
∈
N
)
]
∩
[
R
e
(
n
)
>
−
1
2
]
{\displaystyle {\bigl [}n\in \mathbb {C} \,\backslash {\bigl (}-{\tfrac {1}{2}}+m{\bigr )}(m\in \mathbb {N} ){\bigr ]}\cap {\bigl [}\mathrm {Re} (n)>-{\tfrac {1}{2}}{\bigr ]}}
Beispielsweise gilt:
∫
0
∞
x
4
{
ϑ
00
[
1
3
π
;
exp
(
−
x
)
]
−
1
}
d
x
=
Γ
(
5
4
)
ζ
(
5
2
)
/
ζ
(
−
3
2
)
[
ζ
(
−
3
2
;
1
3
)
+
ζ
(
−
3
2
;
2
3
)
]
{\displaystyle \int _{0}^{\infty }{\sqrt[{4}]{x}}\{\vartheta _{00}[{\tfrac {1}{3}}\pi ;\exp(-x)]-1\}\,\mathrm {d} x=\Gamma ({\tfrac {5}{4}})\zeta ({\tfrac {5}{2}})/\zeta (-{\tfrac {3}{2}}){\bigl [}\zeta (-{\tfrac {3}{2}};{\tfrac {1}{3}})+\zeta (-{\tfrac {3}{2}};{\tfrac {2}{3}}){\bigr ]}}
Die Hurwitzsche Zetafunktion selbst ist so über die Abel-Plana-Summenformel definiert:
ζ
(
y
;
z
)
=
z
1
−
y
y
−
1
+
1
2
z
y
+
2
z
y
−
1
∫
0
∞
sin
[
y
arctan
(
x
)
]
(
x
2
+
1
)
y
/
2
[
exp
(
2
π
x
z
)
−
1
]
d
x
{\displaystyle \zeta (y;z)={\frac {z^{1-y}}{y-1}}+{\frac {1}{2z^{y}}}+{\frac {2}{z^{y-1}}}\int \limits _{0}^{\infty }{\frac {\sin {\bigl [}y\arctan(x){\bigr ]}}{{(x^{2}+1)}^{y/2}{\bigl [}\exp(2\pi xz)-1{\bigr ]}}}\,\mathrm {d} x}
Leonardo Fibonacci John Pell Unendliche Summe[ 37] [ 38] Fibonacci-Zahlen :
∑
n
=
1
∞
1
F
2
n
−
1
=
5
2
∑
n
=
1
∞
2
(
Φ
−
2
)
n
−
1
/
2
1
+
(
Φ
−
2
)
2
n
−
1
=
5
4
∑
a
=
−
∞
∞
2
(
Φ
−
2
)
a
−
1
/
2
1
+
(
Φ
−
2
)
2
a
−
1
=
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{2}}\,\sum _{n=1}^{\infty }{\frac {2(\Phi ^{-2})^{n-1/2}}{1+(\Phi ^{-2})^{2n-1}}}={\frac {\sqrt {5}}{4}}\sum _{a=-\infty }^{\infty }{\frac {2(\Phi ^{-2})^{a-1/2}}{1+(\Phi ^{-2})^{2a-1}}}=}
=
5
4
ϑ
10
(
Φ
−
2
)
2
=
5
8
[
ϑ
00
(
Φ
−
1
)
2
−
ϑ
01
(
Φ
−
1
)
2
]
{\displaystyle ={\frac {\sqrt {5}}{4}}\,\vartheta _{10}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{8}}{\bigl [}\vartheta _{00}(\Phi ^{-1})^{2}-\vartheta _{01}(\Phi ^{-1})^{2}{\bigr ]}}
Dabei ist
Φ
=
5
+
1
2
{\displaystyle \Phi ={\tfrac {{\sqrt {5}}+1}{2}}}
goldene Zahl .
Unendliche Summe der Kehrwerte von den Quadraten der Fibonacci-Zahlen:
∑
n
=
1
∞
1
F
n
2
=
5
24
[
2
ϑ
10
(
Φ
−
2
)
4
−
ϑ
00
(
Φ
−
2
)
4
+
1
]
=
5
24
[
ϑ
00
(
Φ
−
2
)
4
−
2
ϑ
01
(
Φ
−
2
)
4
+
1
]
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{24}}{\bigl [}2\vartheta _{10}(\Phi ^{-2})^{4}-\vartheta _{00}(\Phi ^{-2})^{4}+1{\bigr ]}={\frac {5}{24}}{\bigl [}\vartheta _{00}(\Phi ^{-2})^{4}-2\vartheta _{01}(\Phi ^{-2})^{4}+1{\bigr ]}}
Unendliche Summe der Kehrwerte ungeradstelliger Pell-Zahlen :
∑
n
=
1
∞
1
P
2
n
−
1
=
1
2
ϑ
10
[
(
2
−
1
)
2
]
2
=
1
2
2
[
ϑ
00
(
2
−
1
)
2
−
ϑ
01
(
2
−
1
)
2
]
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{P_{2n-1}}}={\frac {1}{\sqrt {2}}}\,\vartheta _{10}{\bigl [}({\sqrt {2}}-1)^{2}{\bigr ]}^{2}={\frac {1}{2{\sqrt {2}}}}{\bigl [}\vartheta _{00}({\sqrt {2}}-1)^{2}-\vartheta _{01}({\sqrt {2}}-1)^{2}{\bigr ]}}
Summenreihen mit einer bezüglich des Summenindex konstanten Basis und einem bezüglich des Summenindex quadratischen Exponenten können stets als elementare Linearkombinationen der Funktion ϑ₀₀ ausgedrückt werden:
∑
k
=
−
∞
∞
x
a
k
2
+
b
k
+
c
=
exp
[
4
a
c
−
b
2
4
a
ln
(
x
)
]
[
−
π
a
ln
(
x
)
]
1
/
2
ϑ
00
{
π
b
2
a
;
exp
[
π
2
a
ln
(
x
)
−
1
]
}
{\displaystyle \sum _{k=-\infty }^{\infty }x^{ak^{2}+bk+c}=\exp {\bigl [}{\frac {4ac-b^{2}}{4a}}\ln(x){\bigr ]}{\bigl [}{\frac {-\pi }{a\ln(x)}}{\bigr ]}^{1/2}\vartheta _{00}{\bigl \{}{\frac {\pi b}{2a}};\exp {\bigl [}{\frac {\pi ^{2}}{a}}\ln(x)^{-1}{\bigr ]}{\bigr \}}}
Dabei muss
x
{\displaystyle x}
Beispielsweise ergibt jene unendliche Summe folgenden Wert:
∑
k
=
−
∞
∞
(
7
11
)
5
k
2
+
3
k
+
2
=
(
7
11
)
31
/
20
(
π
5
)
1
/
2
ln
(
11
7
)
−
1
/
2
ϑ
00
{
3
π
10
;
exp
[
1
5
π
2
ln
(
7
11
)
−
1
]
}
{\displaystyle \sum _{k=-\infty }^{\infty }{\bigl (}{\frac {7}{11}}{\bigr )}^{5k^{2}+3k+2}={\bigl (}{\frac {7}{11}}{\bigr )}^{31/20}{\bigl (}{\frac {\pi }{5}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {11}{7}}{\bigr )}^{-1/2}\vartheta _{00}{\bigl \{}{\frac {3\pi }{10}};\exp {\bigl [}{\frac {1}{5}}\pi ^{2}\ln {\bigl (}{\frac {7}{11}}{\bigr )}^{-1}{\bigr ]}{\bigr \}}}
Die Greensche Funktion des Laplace-Operators auf dem Rechteck mit den Seiten a und b lautet:[ 39]
G
(
x
,
y
,
x
′
,
y
′
)
=
1
2
π
Re
ln
{
ϑ
11
[
π
2
a
(
x
+
i
y
+
x
′
−
i
y
′
)
,
exp
(
−
π
b
/
a
)
]
ϑ
11
[
π
2
a
(
x
+
i
y
−
x
′
+
i
y
′
)
,
exp
(
−
π
b
/
a
)
]
ϑ
11
[
π
2
a
(
x
+
i
y
−
x
′
−
i
y
′
)
,
exp
(
−
π
b
/
a
)
]
ϑ
11
[
π
2
a
(
x
+
i
y
+
x
′
+
i
y
′
)
,
exp
(
−
π
b
/
a
)
]
}
{\displaystyle G(x,y,x',y')={\frac {1}{2\pi }}\operatorname {Re} \ln {\biggl \{}{\frac {\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy+x'-iy'),\exp(-\pi b/a)]\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy-x'+iy'),\exp(-\pi b/a)]}{\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy-x'-iy'),\exp(-\pi b/a)]\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy+x'+iy'),\exp(-\pi b/a)]}}{\biggr \}}}
Dieser Ausdruck liefert das Potential der Linienladung am Ort (
0
<
x
<
a
{\displaystyle 0<x<a}
0
<
y
<
b
{\displaystyle 0<y<b}
0
<
x
′
<
a
{\displaystyle 0<x'<a}
0
<
y
′
<
b
{\displaystyle 0<y'<b}
Die allgemeine quintische Gleichung kann nach dem Satz von Abel-Ruffini nicht elementar radikalisch gelöst werden. Aber eine allgemeine Lösung ist sehr wohl mit Hilfe der elliptischen Funktionen möglich. Mit der Thetafunktion kann auch der Allgemeinfall der Gleichung fünften Grades in Abhängigkeit vom elliptischen Nomen aus einem von den Koeffizienten stets elementar abhängigen elliptischen Modul gelöst werden. Hierbei werden die fünften Potenz und die fünfte Wurzel des betroffenen elliptischen Nomens[ 40] Bring-Jerrard-Form kann die allgemeine Lösung mit der Thetafunktion ϑ₀₀ vereinfacht dargestellt werden:
x
5
+
5
x
=
4
c
{\displaystyle x^{5}+5\,x=4\,c}
Für alle reellen Werte
c
{\displaystyle c}
identischer Abbildungsfunktion für
x
{\displaystyle x}
c
{\displaystyle c}
x
{\displaystyle x}
c
{\displaystyle c}
Lösungsverfahren der quintischen Gleichungen über die Thetafunktion
Bring-Jerrard-Gleichung:
x
5
+
5
x
=
4
c
{\displaystyle x^{5}+5\,x=4\,c}
Elliptischer Nomen-q-Funktionswert:
Q
=
q
[
(
2
c
2
+
2
+
2
c
4
+
1
)
−
1
/
2
(
c
4
+
1
+
1
+
c
)
]
=
q
{
c
t
l
h
[
1
2
a
c
l
h
(
c
)
]
2
}
{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}=q{\bigl \{}\mathrm {ctlh} {\bigl [}{\tfrac {1}{2}}\mathrm {aclh} (c){\bigr ]}^{2}{\bigr \}}}
Die reelle Lösung für x:
x
=
[
ϑ
00
(
Q
1
/
5
)
2
−
5
ϑ
00
(
Q
5
)
2
]
ϑ
00
(
Q
1
/
5
)
2
+
5
ϑ
00
(
Q
5
)
2
−
4
ϑ
00
(
Q
)
2
−
2
ϑ
00
(
Q
1
/
5
)
ϑ
00
(
Q
5
)
4
ϑ
10
(
Q
)
ϑ
01
(
Q
)
ϑ
00
(
Q
)
=
{\displaystyle x={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{4\,\vartheta _{10}(Q)\,\vartheta _{01}(Q)\,\vartheta _{00}(Q)}}=}
=
[
ϑ
00
(
Q
1
/
5
)
2
−
5
ϑ
00
(
Q
5
)
2
]
ϑ
00
(
Q
1
/
5
)
2
+
5
ϑ
00
(
Q
5
)
2
−
4
ϑ
00
(
Q
)
2
−
2
ϑ
00
(
Q
1
/
5
)
ϑ
00
(
Q
5
)
2
2
c
4
+
1
−
2
c
2
ϑ
00
(
Q
)
3
=
{\displaystyle ={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{2\,{\sqrt {2\,{\sqrt {c^{4}+1}}-2\,c^{2}}}\,\vartheta _{00}(Q)^{3}}}=}
=
256
c
ϑ
00
(
Q
)
12
(
c
4
+
1
+
c
2
)
2
[
ϑ
00
(
Q
1
/
5
)
2
−
5
ϑ
00
(
Q
5
)
2
]
4
[
ϑ
00
(
Q
1
/
5
)
2
+
5
ϑ
00
(
Q
5
)
2
−
4
ϑ
00
(
Q
)
2
−
2
ϑ
00
(
Q
1
/
5
)
ϑ
00
(
Q
5
)
]
2
+
320
ϑ
00
(
Q
)
12
{\displaystyle ={\frac {256\,c\,\vartheta _{00}(Q)^{12}}{{\bigl (}{\sqrt {c^{4}+1}}+c^{2}{\bigr )}^{2}{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}^{4}{\bigl [}\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5}){\bigr ]}^{2}+320\,\vartheta _{00}(Q)^{12}}}}
Der Ausdruck ctlh steht für den Cotangens lemniscatus hyperbolicus und der Ausdruck aclh steht für den Areacosinus lemniscatus hyperbolicus.
Für weitere Informationen über diese beiden Funktionen, siehe Artikel Hyperbolisch lemniskatischer Sinus .
Im Folgenden wird ein nicht elementar darstellbarer, aber algebraischer Beispielwert behandelt, der mit dem gezeigten Algorithmus hervorgebracht werden kann:
x
5
+
5
x
=
4
{\displaystyle x^{5}+5\,x=4}
Q
=
q
[
(
2
c
2
+
2
+
2
c
4
+
1
)
−
1
/
2
(
c
4
+
1
+
1
+
c
)
]
(
c
=
1
)
=
q
[
2
4
2
+
sin
(
π
8
)
]
{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c=1{\bigr )}=q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}{\bigr )}{\bigr ]}}
Q
≈
0.18520287008030014142515182307361246060360377625
{\displaystyle Q\approx 0.18520287008030014142515182307361246060360377625}
x
=
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
1
/
5
}
2
−
5
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
5
}
2
4
ϑ
10
{
q
[
2
4
2
+
sin
(
π
8
)
]
}
ϑ
01
{
q
[
2
4
2
+
sin
(
π
8
)
]
}
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
}
×
{\displaystyle x={\frac {\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}^{1/5}\}^{2}-5\,\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}^{5}\}^{2}}{4\,\vartheta _{10}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}\,\vartheta _{01}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}\,\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}}}\times }
×
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
1
/
5
}
2
+
5
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
5
}
2
−
4
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
}
2
−
2
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
1
/
5
}
ϑ
00
{
q
[
2
4
2
+
sin
(
π
8
)
]
5
}
{\displaystyle \times {\sqrt {\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{1/5}\}^{2}+5\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{5}\}^{2}-4\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}\}^{2}-2\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{1/5}\}\,\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{5}\}}}}
x
≈
0.75192639869405948026865366345020738740978383913
{\displaystyle x\approx 0.75192639869405948026865366345020738740978383913}
Im Folgenden wird ein weiterer nicht elementar darstellbarer algebraischer Beispielwert behandelt. Die Gleichung
x
5
+
40
x
=
32
{\displaystyle x^{5}+40\,x=32}
(
2
−
3
/
4
x
)
5
+
5
(
2
−
3
/
4
x
)
=
4
(
2
−
3
/
4
)
{\displaystyle {\bigl (}2^{-3/4}\,x{\bigr )}^{5}+5\,{\bigl (}2^{-3/4}\,x{\bigr )}=4\,{\bigl (}2^{-3/4}{\bigr )}}
c
=
2
−
3
/
4
{\displaystyle c=2^{-3/4}}
Q
=
q
[
(
2
c
2
+
2
+
2
c
4
+
1
)
−
1
/
2
(
c
4
+
1
+
1
+
c
)
]
(
c
=
2
−
3
/
4
)
=
q
[
cos
(
1
8
π
)
]
{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c=2^{-3/4}{\bigr )}=q{\bigl [}\cos {\bigl (}{\tfrac {1}{8}}\pi {\bigr )}{\bigr ]}}
Q
≈
0,117
8579353118577191415525411064892354454594487939419613
{\displaystyle Q\approx 0{,}1178579353118577191415525411064892354454594487939419613}
Dieses wird nun in die genannte Beispielgleichung eingesetzt:
Quintische Gleichung mit zugehöriger reeller Lösung
Quintische Gleichung:
x
5
+
40
x
=
32
{\displaystyle x^{5}+40\,x=32}
Reelle Lösung von dieser Gleichung dargestellt über die Thetafunktion:
x
=
ϑ
00
{
q
[
cos
(
1
8
π
)
]
1
/
5
}
2
−
5
ϑ
00
{
q
[
cos
(
1
8
π
)
]
5
}
2
2
ϑ
00
{
q
[
cos
(
1
8
π
)
]
}
3
×
{\displaystyle x={\frac {\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}^{2}-5\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}^{2}}{{\sqrt {2}}\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}{\bigr \}}^{3}}}\times }
×
ϑ
00
{
q
[
cos
(
1
8
π
)
]
1
/
5
}
2
+
5
ϑ
00
{
q
[
cos
(
1
8
π
)
]
5
}
2
−
4
ϑ
00
{
q
[
cos
(
1
8
π
)
]
}
2
−
2
ϑ
00
{
q
[
cos
(
1
8
π
)
]
1
/
5
}
ϑ
00
{
q
[
cos
(
1
8
π
)
]
5
}
{\displaystyle \times {\sqrt {\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}^{2}+5\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}^{2}-4\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}{\bigr \}}^{2}-2\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}}}}
Für diese Lösung beziehungsweise diese Zahl ist jegliche elementare Darstellung unmöglich.
Genähert ergibt sich:
x
≈
0,792
19966455364397976012391796828231319392199994056182
{\displaystyle x\approx 0{,}79219966455364397976012391796828231319392199994056182}
Charles Hermite Erland Samuel Bring Der Mathematiker Paolo Ruffini veröffentlichte 1799 einen lückenhaften Beweis für die Unauflösbarkeit der allgemeinen quintischen Gleichung über elementare Wurzelausdrücke. Er beschäftigte sich als Erster mit dem Beweis dieser These und er wendete in seinem Beweis die Gesetze der Gruppentheorie an. Im Jahre 1824 brachte Niels Henrik Abel einen vollständigen Beweis für diese elementare Unlösbarkeit der verallgemeinerten Gleichungen fünften Grades. Um 1830 stellte der französische Mathematiker Évariste Galois die nach ihm benannte Theorie über die Lösbarkeitskriterien von quintischen Gleichungen und höher gradigen Gleichungen über elementare Wurzelausdrücke auf. Diese Theorie wird Galois-Theorie genannt. Später erforschte der ebenso aus Frankreich kommende Mathematiker Charles Hermite bei der Bring-Jerrard-Form der quintischen Gleichung mit gleichem Vorzeichen vor quintischem und linearem Glied einen Algorithmus für die Ermittlung des elliptischen Moduls beziehungsweise der numerischen Exzentrizität für den Ausdruck der Lösung mittels elliptischer Modulfunktionen. Die Tatsache, dass für die Darstellung des Bringschen Radikals über Modulfunktionen der Modul genau dem gezeigten Cotangens-lemniscatus-hyperbolicus-Quadrat entspricht, wurde durch ihn erkannt. Hermite schrieb diesen Zusammenhang in seiner Arbeit Sur la résolution de l’Équation du cinquiéme degré Comptes rendus nieder. Die italienische Version seiner Arbeit Sulla risoluzione delle equazioni del quinto grado enthält auf der Seite 258 diejenige Formel, aus welcher der hier genannte Modul hervorgeht. Ebenso analysierten die Mathematiker John Stuart Glashan, George Paxton Young[ 41] Carl Runge [ 42]
x
5
+
5
x
=
4
c
{\displaystyle x^{5}+5\,x=4\,c}
x
=
2
5
y
−
1
/
4
50
+
75
y
−
50
y
2
4
cosh
{
1
5
arcosh
[
5
5
+
5
y
2
(
1
+
2
y
)
4
+
6
y
−
4
y
2
]
}
−
{\displaystyle x={\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{50+75y-50y^{2}}}\cosh {\biggl \{}{\frac {1}{5}}\operatorname {arcosh} {\biggl [}{\frac {5{\sqrt {5+5y^{2}}}}{(1+2y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}-}
−
2
5
y
−
1
/
4
50
+
75
y
−
50
y
2
4
sinh
{
1
5
arsinh
[
5
y
5
+
5
y
2
(
2
−
y
)
4
+
6
y
−
4
y
2
]
}
{\displaystyle -{\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{50+75y-50y^{2}}}\sinh {\biggl \{}{\frac {1}{5}}\operatorname {arsinh} {\biggl [}{\frac {5y{\sqrt {5+5y^{2}}}}{(2-y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}}
Zugehöriger elliptischer Schlüssel:
y
=
W
R
5
[
(
2
c
2
+
2
+
2
c
4
+
1
)
−
1
/
2
(
c
4
+
1
+
1
+
c
)
]
=
W
R
5
{
c
t
l
h
[
1
2
a
c
l
h
(
c
)
]
2
}
{\displaystyle y=W_{R5}{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}=W_{R5}{\bigl \{}\mathrm {ctlh} {\bigl [}{\tfrac {1}{2}}\mathrm {aclh} (c){\bigr ]}^{2}{\bigr \}}}
Der große W -Buchstabe stellt die große reduzierte webersche Modulfunktion dar. Generell dient das Bringsche Radikal zum Lösen der verallgemeinerten Gleichung fünften Grades und wurde vom schwedischen Mathematiker Erland Samuel Bring erforscht. Der gezeigte elliptische Schlüssel ermöglichte die Lösung der allgemeinen Bring-Jerrard-Form nach dem Muster von den Mathematikern Glashan, Young und Runge. Mit der elliptischen Identität des Bringschen Radikals beschäftigten sich außerdem die russischen Mathematiker Viktor Prasolov und Yuri Solovyev in ihrem Werk Elliptic Functions and Elliptic Integrals aus dem Jahre 1991. Und basierend auf den Aufsätzen von Soon Yi Kang und Nikolaos Bagis kann über den gezeigten Lösungausdruck mit dem elliptischen Schlüssel ein Lösungsausdruck derselben Lösung über die Rogers-Ramanujan-Kettenbrüche R und S hergeleitet werden.
Die Hermitesche elliptische phi-Funktion ist so definiert:
φ
H
(
x
)
=
ϑ
10
(
x
)
1
/
2
ϑ
00
(
x
)
−
1
/
2
{\displaystyle \varphi _{H}(x)=\vartheta _{10}(x)^{1/2}\,\vartheta _{00}(x)^{-1/2}}
Mit folgender Formel über Phifunktion, Thetafunktion und Theta-Ableitungsfunktion lassen sich viele exemplarische Formeln rein algebraischer Art erzeugen, die sehr schnell exakt zur Kreiszahl konvergieren. Dieses Verfahren wurde durch Ramanujan entdeckt und in seinen Aufzeichnungen im Jahre 1814 niedergeschrieben. Die Gebrüder Borwein fassten seine Niederschriften auf und verwendeten die Elliptische Alphafunktion zur Beschreibung seiner Resultate. Vereinfacht soll die Formel, mit der Srinivasa Ramanujan gearbeitet hat, mit Hilfe der genannten Funktionen dargestellt werden:
1
π
=
∑
n
=
0
∞
(
4
n
)
!
sin
{
4
arctan
[
φ
H
(
x
)
4
]
}
2
n
256
n
(
n
!
)
4
×
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {(4n)!\sin {\bigl \{}4\arctan {\bigl [}\varphi _{H}(x)^{4}{\bigr ]}{\bigr \}}^{2n}}{256^{n}(n!)^{4}}}\times }
×
⟨
π
−
1
ϑ
00
(
x
)
−
4
[
1
+
φ
H
(
x
)
8
]
−
π
−
1
ln
(
1
/
x
)
[
1
+
φ
H
(
x
)
8
]
2
{
4
x
ϑ
01
′
(
x
)
[
1
+
φ
H
(
x
)
8
]
ϑ
01
(
x
)
ϑ
00
(
x
)
4
+
2
φ
H
(
x
)
8
}
+
π
−
1
ln
(
1
/
x
)
cos
{
4
arctan
[
φ
H
(
x
)
4
]
}
n
⟩
{\displaystyle \times {\biggl \langle }{\frac {\pi ^{-1}\vartheta _{00}(x)^{-4}}{[1+\varphi _{H}(x)^{8}]}}-{\frac {\pi ^{-1}\ln(1/x)}{[1+\varphi _{H}(x)^{8}]^{2}}}{\biggl \{}{\frac {4x\vartheta '_{01}(x)[1+\varphi _{H}(x)^{8}]}{\vartheta _{01}(x)\vartheta _{00}(x)^{4}}}+2\varphi _{H}(x)^{8}{\biggr \}}+\pi ^{-1}\ln(1/x)\cos {\bigl \{}4\arctan {\bigl [}\varphi _{H}(x)^{4}{\bigr ]}{\bigr \}}n{\biggr \rangle }}
Diese Formeln ist für alle Werte
0
<
x
<
exp
(
−
2
π
)
{\displaystyle 0<x<\exp(-{\sqrt {2}}\,\pi )}
Tabellarisch werden hiermit einzelne Exemplare von elliptischem Modul und zugehöriger Kreiszahlformel aufgelistet. Dabei wird der jeweilige Nomenwert x in der linken Spalte und die daraus resultierende Kreiszahlsummenformel in der rechten Spalte angegeben:
Elliptisches Nomen
Kreiszahlformel
x
=
exp
(
−
6
π
)
{\displaystyle x=\exp(-{\sqrt {6}}\,\pi )}
1
π
=
∑
n
=
0
∞
(
4
n
)
!
(
1
+
8
n
)
2
3
(
n
!
)
4
48
2
n
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {(4n)!(1+8n)}{2{\sqrt {3}}(n!)^{4}48^{2n}}}}
x
=
exp
(
−
10
π
)
{\displaystyle x=\exp(-{\sqrt {10}}\,\pi )}
1
π
=
∑
n
=
0
∞
2
2
(
4
n
)
!
(
1
+
10
n
)
9
(
n
!
)
4
12
4
n
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {2{\sqrt {2}}(4n)!(1+10n)}{9(n!)^{4}12^{4n}}}}
x
=
exp
(
−
3
2
π
)
{\displaystyle x=\exp(-3{\sqrt {2}}\,\pi )}
1
π
=
∑
n
=
0
∞
3
3
(
4
n
)
!
(
3
+
40
n
)
49
(
n
!
)
4
28
4
n
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {3{\sqrt {3}}(4n)!(3+40n)}{49(n!)^{4}28^{4n}}}}
x
=
exp
(
−
22
π
)
{\displaystyle x=\exp(-{\sqrt {22}}\,\pi )}
1
π
=
∑
n
=
0
∞
(
4
n
)
!
(
19
+
280
n
)
18
11
(
n
!
)
4
1584
2
n
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {(4n)!(19+280n)}{18{\sqrt {11}}(n!)^{4}1584^{2n}}}}
x
=
exp
(
−
58
π
)
{\displaystyle x=\exp(-{\sqrt {58}}\,\pi )}
1
π
=
∑
n
=
0
∞
2
2
(
4
n
)
!
(
1103
+
26390
n
)
9801
(
n
!
)
4
396
4
n
{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {2{\sqrt {2}}(4n)!(1103+26390n)}{9801(n!)^{4}396^{4n}}}}
Die zuletzt genannte Formel ist die berühmteste unter diesen Formeln und erlangte große internationale Bekanntheit unter den Mathematikern.
Niels Henrik Abel : Solution de quelques problèmes à l’aide d’intégrales définies . Magazin for Naturvidenskaberne, Argang I, Bind2, Christina, 1823N. I. Akhiezer : Elements of the Theory of Elliptic Functions , AMS Translations of Mathematical Monographs, Band 79, 1990, AMS, Rhode Island, ISBN 0-8218-4532-2 (russisches Original Moskau 1970).George E. Andrews : A simple proof of Jacobi´s triple product identity. In: Proceedings of the American Mathematical Society .doi:10.1090/S0002-9939-1965-0171725-X .Tom M. Apostol : Modular Functions and Dirichlet Series in Number Theory . Springer-Verlag, New York 1990, ISBN 0-387-97127-0 .Tom M. Apostol : Introduction to Analytic Number Theory. Springer, New York NY u. a. 1976, ISBN 0-387-90163-9 , S. 319.Hershel Farkas , Harry Rauch : Theta Functions with Applications to Riemann Surfaces . Williams & Wilkins, Baltimore 1974.Hershel Farkas , Irwin Kra : Riemann Surfaces . Springer Verlag, Graduate Texts in Mathematics, 1980 (Kapitel 6)Adolf Hurwitz : Vorlesungen über Allgemeine Funktionentheorie und elliptische Funktionen . Springer-Verlag, Berlin / Heidelberg / New York 2000, ISBN 3-540-63783-4 .Dale Husemöller : Elliptic Curves . Springer Verlag, Berlin / Heidelberg / New York 2004, ISBN 0-387-95490-2 .Jun-Ichi Igusa : Theta Functions . Grundlehren der mathematischen Wissenschaften. Springer Verlag, 1972.Max Koecher , Aloys Krieg : Elliptische Funktionen und Modulformen . 2. Auflage. Springer-Verlag, Berlin / Heidelberg / New York 2007, ISBN 3-540-63744-3 .Adolf Krazer : Lehrbuch der Thetafunktionen .David Mumford Tata Lectures on Theta , Band 1, 3. Auflage. Springer Verlag 1994 (insgesamt drei Bände).Reinhold Remmert : Funktionentheorie I. Springer-Verlag Berlin Heidelberg New York 1989, ISBN 3-540-51238-1 .Tom M. Apostol : Hurwitz zeta function . In Olver, Lozier, Boisvert, Clark: NIST Handbook of Mathematical Functions . Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248Bruno Schoeneberg : Elliptic Modular Functions . Grundlehren der mathematischen Wissenschaften. Springer Verlag, 1974 (Kapitel 9, Theta Series ).Edmund T. Whittaker , George Neville Watson : A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990. S. 469–470.Charles Hermite : Sur la résolution de l’Équation du cinquiéme degré Comptes rendus , Comptes Rendus Acad. Sci. Paris, Nr. 11, März 1858.Tafelwerke:
Aufsätze und Buchbeiträge, die im Artikel benutzt wurden:
Jonathan Borwein und Peter Borwein : π and the AGM: A study in Analytic Number Theory and Computational Complexity . Wiley-Interscience, 1987. S. 94–97.Jonathan Borwein und Peter Borwein: Theta Functions and the Arithmetic-Geometric Mean Iteration . Ch. 2 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, S. 33–61, 1987.
Jonathan Borwein, Peter Borwein und David Bailey: Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi . Amer. Math. Monthly 96, 201–219, 1989.
Soon Yi Kang: Ramanujan’s Formulas For Explicit Evaluation Of The Rogers-Ramanujan Continued Fraction And Theta-Functions . Acta Arithmetica, Band 90, 1999, S. 49–68.
Nickos Papadatos: The characteristic function of the discrete Cauchy distribution . Kapodistrias-Universität Athen , 2018, Arxiv.
Srinivasa Ramanujan : Modular Equations and Approximations to π. Quart. J. Pure. Appl. Math. Auflage 45, 350–372, 1913–1914.J. D. Fenton and R. S. Gardiner-Garden: Rapidly-convergent methods for evaluating elliptic integrals and theta and elliptic functions . J. Austral. Math. Soc. (Series B) 24, 1982, S. 48 und 49.
Maxie D. Schmidt: Square series generating function transformations. Journal of Inequalities and Special Functions, Band 8, 2017, Heft 2, Arxiv 2016.
Nikolaos Bagis: On the complete solution of the general quintic using the Rogers-Ramanujan continued fraction . Arxiv 2015.
Michael Trott: Modular Equations of the Rogers-Ramanujan Continued Fraction , Mathematica, Band 9, 2004, S. 314–333.
Frank Olver : Asymptotics and special functions . Reprint of the 1974 original. AKP Classics. A K Peters, Ltd., Wellesley, MA, 1997.Sylvie Corteel und Jeremy Lovejoy: Overpartitions . Versailles/Talence, Frankreich 2004, S. 1–13.
Harold Mortimer Edwards: Riemann's Zeta Function . New York: Dover, 2001.
Jinhee Yi: Theta-function identities and the explicit formulas for theta-function and their applications . Journal of Mathematical Analysis and Applications , Band 292, Nr. 2, 2004, S. 381–400.
↑ Carl Gustav Jacobi: Theorie der elliptischen Funktionen aus den Eigenschaften der Thetareihe abgeleitet. Vorlesungsausarbeitung von Karl Wilhelm Borchardt 1838. In: Jacobi: Werke , Band 1, 1881 (Herausgeber Borchardt, Karl Weierstraß ), S. 497–538.
↑ Carl Ludwig Siegel : Lectures on Complex Function Theory . Band 2. Wiley-Interscience, 1971, S. 163.↑ Eric W. Weisstein : Jacobi Theta Functions .MathWorld ↑ http://wayback.cecm.sfu.ca/~pborwein/TEMP_PROTECTED/pi-agm.pdf ↑ DLMF: 20.5 Infinite Products and Related Results. Abgerufen am 13. August 2022 . ↑ Wolfram Research: Elliptic Theta Prime. Derivative of the Jacobi theta function ϑ4 . Introduction to the Jacobi theta functions. Abgerufen am 18. Juli 2021 . ↑ https://metaphor.ethz.ch/x/2019/fs/401-4110-19L/sc/talk4.pdf ↑ DLMF: 20.7 Identities. Abgerufen am 13. August 2022 . ↑ https://arxiv.org/pdf/1806.08474.pdf ↑ https://www.researchgate.net/profile/Toshio-Fukushima/publication/226331661_Fast_computation_of_complete_elliptic_integrals_and_Jacobian_elliptic_functions/links/0fcfd50b44bb3e76b9000000/Fast-computation-of-complete-elliptic-integrals-and-Jacobian-elliptic-functions.pdf?origin=publication_detail ↑ https://www.math.lsu.edu/~mahlburg/preprints/4.pdf ↑ Elsevier Enhanced Reader. Abgerufen am 14. August 2022 (englisch). ↑ code golf - Strict partitions of a positive integer. Abgerufen am 9. März 2022 . ↑ A000009 - OEIS. Abgerufen am 9. März 2022 . ↑ Eric W. Weisstein: Partition Function Q. Abgerufen am 9. März 2022 (englisch). ↑ Eric W. Weisstein: Partition Function P. Abgerufen am 11. März 2022 (englisch). ↑ Eric W. Weisstein: Partition Function Q. Abgerufen am 11. März 2022 (englisch). ↑ Eric W. Weisstein : Ramanujan g- and G-Functions .MathWorld ↑ a b Eric W. Weisstein : Dedekind Eta Function .MathWorld ↑ Eric W. Weisstein : q-Pochhammer Symbol .MathWorld ↑ https://vdoc.pub/download/a-brief-introduction-to-theta-functions-6v41da306900 ↑ https://www.researchgate.net/publication/235432739_Ramanujan%27s_theta-function_identities_involving_Lambert_series ↑ Jinhee Yi: Theta-function identities and the explicit formulas for theta-function and their applications . In: Journal of Mathematical Analysis and Applications Band 292 , Nr. 2 , 15. April 2004, ISSN 0022-247X S. 381–400 , doi :10.1016/j.jmaa.2003.12.009 sciencedirect.com [abgerufen am 21. Juli 2021]).
↑ Bruce C. Berndt, Örs Rebák: Explicit values for Ramanujan's theta function φ(q) . 9. Januar 2022, ISSN 2804-7370 doi :10.46298/hrj.2022.8923 uit.no [abgerufen am 23. April 2022]).
↑ Eric W. Weisstein: Elliptic Integral Singular Value. Abgerufen am 3. Juni 2022 (englisch). ↑ Eric W. Weisstein: Elliptic Alpha Function. Abgerufen am 30. Juni 2022 (englisch). ↑ Eric W. Weisstein: Elliptic Delta Function. Abgerufen am 30. Juni 2022 (englisch). ↑ Andreas Dieckmann: Table of Infinite Products Infinite Sums Infinite Series, Elliptic Theta.
↑ Eric W. Weisstein : Elliptic Integral Singular Value .MathWorld ↑ Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Kapitel 16", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , New York: Dover, S. 578, ISBN 978-0-486-61272-0 , MR 0167642.
↑ Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products , 6th ed. San Diego, CA: Academic Press, 2000, p. xxxiv.
↑ DLMF: 20.13 Physical Applications. Abgerufen am 13. August 2022 . ↑ Yousuke Ohyama: Differential relations of theta functions . In: Osaka Journal of Mathematics . Band 32 , Nr. 2 , Januar 1995, ISSN 0030-6126 S. 431–450 (projecteuclid.org [abgerufen am 10. März 2022]).
↑ Eric W. Weisstein : Elliptic Alpha Function .MathWorld ↑ integration - Curious integrals for Jacobi Theta Functions $\int_0^1 \vartheta_n(0,q)dq$. Abgerufen am 13. August 2022 (englisch). ↑ DLMF: 20.10 Integrals. Abgerufen am 13. August 2022 . ↑ Landau (1899) zitiert nach Borwein , Page 94, Exercise 3.
↑ Number-theoretical, combinatorial and integer functions – mpmath 1.1.0 documentation. Abgerufen am 18. Juli 2021 . ↑ EllipticTheta. Wolfram Research, Inc. Abgerufen am 29. September 2022 . ↑ R. B. King, E. R. Canfield: Icosahedral symmetry and the quintic equation . In: Computers & Mathematics with Applications . Band 24 , Nr. 3 , 1. August 1992, ISSN 0898-1221 S. 13–28 (sciencedirect.com [abgerufen am 2. Juni 2023]).
↑ G. P. Young: Solution of Solvable Irreducible Quintic Equations, Without the Aid of a Resolvent Sextic. In: Amer. J. Math. Band 7, Seiten 170–177, 1885.
↑ C. Runge: Über die auflösbaren Gleichungen von der Form
x
5
+
u
x
+
v
=
0
{\displaystyle x^{5}+ux+v=0}
In: Acta Math. Band 7, Seiten 173–186, 1885, doi:10.1007/BF02402200 .

































![{\displaystyle \vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c5acc090a4c8a2327974fa27125ca0f796ce535)
![{\displaystyle \vartheta _{01}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n-1}+w^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ceef12dd801305a4cf783265e8e157f4bdffde)
![{\displaystyle \vartheta _{10}(v;w)=2w^{1/4}\cos(v)\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n}+w^{4n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a19ed41533c1761bf80ff54c7445c2518b5fe6)
![{\displaystyle \vartheta _{11}(v;w)=-2w^{1/4}\sin(v)\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n}+w^{4n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92629da82416bb2f1c85e98624b798f5ef148eb)



![{\displaystyle \vartheta _{00}[\pi z;\exp(i\pi \tau )]=\Theta _{0,0}(z,\tau )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c809bb2e936986a0f84e2494561eafcbc1273c23)
![{\displaystyle \vartheta _{01}[\pi z;\exp(i\pi \tau )]=\Theta _{0,1}(z,\tau )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d726000de207acacf4423477bc46a50bd44115af)
![{\displaystyle \vartheta _{10}[\pi z;\exp(i\pi \tau )]=\Theta _{1,0}(z,\tau )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17d04da1b88a43174ffb5670b50986d2ba0d6924)
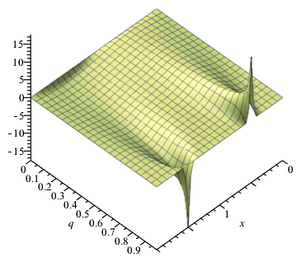






































![{\displaystyle \vartheta (z,\tau )=\prod _{n=1}^{\infty }(1-e^{2\pi in\tau })(1+e^{\pi i[(2n-1)\tau +2z]})(1+e^{\pi i[(2n-1)\tau -2z]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba92fb9c6005d5b6f4178d2b438abfcb42bac492)



![{\displaystyle \vartheta _{00}(x)=1+{\frac {4x}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp(-y^{2})\{1-x^{2}\cos[2{\sqrt {\ln(1/x)}}\,y]\}}{1-2x^{2}\cos[2{\sqrt {\ln(1/x)}}\,y]+x^{4}}}\,\mathrm {d} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0d71f2e3ff6e308182f3ef522c6814a90c86133)







![{\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n}}\right)\right]^{2}=\lim _{n\rightarrow \infty }{\frac {1}{n}}\sum _{k=-\infty }^{\infty }\operatorname {sech} \left({\frac {k}{n}}\right)=\int _{-\infty }^{\infty }\operatorname {sech} (x)\,\mathrm {d} x=\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f527f446d7cb296589813aba1b9dfe810841131a)

![{\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{n^{\color {ForestGreen}2}}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{\color {ForestGreen}2}}}\right)\right]^{2}=\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad54dbf35aadfb45f382f1d877a635ca6c00a40)
![{\displaystyle {\color {Navy}\lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{2}}}\right)\right]}={\sqrt {\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1f216d8ec4abedfd457dea6c2223576ba8ec7f9)
![{\displaystyle {\color {Navy}\lim _{n\rightarrow \infty }{\frac {1}{n}}\vartheta _{00}\left[\exp \left(-{\frac {1}{n^{2}}}\right)\right]}=\lim _{n\rightarrow \infty }{\frac {1}{n}}\sum _{k=-\infty }^{\infty }\exp \left[-\left({\frac {k}{n}}\right)^{2}\right]=\int _{-\infty }^{\infty }\exp(-x^{2})\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05229371f0733320e25adc5c9bf43e1e52d410e1)

![{\displaystyle \vartheta _{00}[q(k)]={\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12b1e4fb729e6f2c922d81f8858191dac117612)
![{\displaystyle \vartheta _{01}[q(k)]={\sqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec20ef56acfd90357a38319f52d6ce54e69cbdcf)
![{\displaystyle \vartheta _{10}[q(k)]={\sqrt {|k|}}\,{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c790e78c97347ccc384b3c80145e814ed12188b4)
![{\displaystyle q(k)=\exp {\biggl [}-\pi \,{\frac {K({\sqrt {1-k^{2}}})}{K(k)}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85afb82649033c19f2f3d779ea5cd4bb7dcda556)
![{\displaystyle K(\varepsilon )={\frac {\pi }{2}}\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}\,\varepsilon ^{2n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8e0bd58bce9d46b748e6487538340503d75abd)































![{\displaystyle \vartheta _{01}(x)={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}{\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1ce0f03f54d5c372a5b45e035f1873a51542d37)

![{\displaystyle (x;x^{2})_{\infty }={\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}=\vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b6a97895e7b968dc44caaaf915cf32f9caf875)
![{\displaystyle (x;x)_{\infty }={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}=\vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f313a9983bb1e83b4650e823753e9c889d9daa09)



![{\displaystyle (x;x)_{\infty }=1+\sum _{n=1}^{\infty }{\bigl [}-x^{{\text{Fn}}(2n-1)}-x^{{\text{Kr}}(2n-1)}+x^{{\text{Fn}}(2n)}+x^{{\text{Kr}}(2n)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab59cb2fcf2f3ddc6f1e10561a526de51f516f3)




![{\displaystyle {\frac {4^{-1/(n+2)}}{n+2}}\csc {\bigl (}{\frac {\pi }{n+2}}{\bigr )}\beta {\biggl [}{\frac {n}{2(n+2)}}{\biggr ]}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{n+2}+1}}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48152e52c3eb9c14398e29907e759b53900153c6)
![{\displaystyle {\frac {1}{\sqrt {x^{4}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c42e35cf46076ad7140865bd7327f051d0af90)

![{\displaystyle {\frac {1}{4{\sqrt {2}}}}\csc {\bigl (}{\frac {\pi }{4}}{\bigr )}\beta {\bigl (}{\frac {1}{4}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={\biggl \{}{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}{\biggr \}}_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8b6e76d56df52d6812600dae1b884435a0fc9e6)


![{\displaystyle {\frac {1}{\sqrt {x^{6}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3186259fdf61a7ebb632f3d02d679cae524c35f7)

![{\displaystyle {\frac {1}{6{\sqrt[{3}]{2}}}}\csc {\bigl (}{\frac {\pi }{6}}{\bigr )}\beta {\bigl (}{\frac {1}{3}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{6}+1}}}\,\mathrm {d} x={\biggl \{}{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}{\biggr \}}_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/299d6833adfa6ef197ec2cb94807c97203cfc731)
![{\displaystyle ={\frac {1}{6}}{\sqrt[{4}]{27}}F{\bigl [}2\arctan({\sqrt[{4}]{3}});{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{9}}{\sqrt[{4}]{27}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{3}}{\sqrt[{4}]{3}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d55b9913617b5871c7a524c0eeec8168828a1c5a)
![{\displaystyle {\color {ForestGreen}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}={\frac {1}{2{\sqrt[{3}]{2}}{\sqrt[{4}]{3}}}}\beta {\bigl (}{\frac {1}{3}}{\bigr )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fffa258bf7309994a5d54ae0f95d4614975d1ec2)
![{\displaystyle {\frac {1}{\sqrt {x^{8}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1e65e8fbe7fe9ec13d33b27e5e11867643b5c2)

![{\displaystyle {\frac {1}{8{\sqrt[{4}]{2}}}}\csc {\bigl (}{\frac {\pi }{8}}{\bigr )}\beta {\bigl (}{\frac {3}{8}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{8}+1}}}\,\mathrm {d} x=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21e13acda89a6825a0a7a6477bf0e2d072b3ce9e)
![{\displaystyle ={\biggl \langle }{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}{\biggr \rangle }_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb6e69df9f354be05ea072d60cefd2fd977b7dbf)
![{\displaystyle ={\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\bigl [}\pi ;2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\bigr ]}={\frac {1}{2}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2{\sqrt {2}}-2}}{\bigr )}=2\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85a8ad3dc4c269cf0392b1260587f5471ae5e932)
![{\displaystyle {\color {ForestGreen}K({\sqrt {2}}-1)={\frac {1}{8}}{\sqrt[{4}]{2}}\,({\sqrt {2}}+1)\,\beta {\bigl (}{\frac {3}{8}}{\bigr )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177a0e98ca0233f21a20d37c9dd285369ecf1cda)

![{\displaystyle q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d8a66693d1cd78fa0422519e6a5f523cfa1f69)

![{\displaystyle \vartheta _{00}[\exp(-\pi )]=\vartheta _{00}[q({\tfrac {1}{2}}{\sqrt {2}})]={\sqrt {2\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}}=2^{-1/2}\pi ^{-1/2}\beta ({\tfrac {1}{4}})^{1/2}=2^{-1/4}{\sqrt[{4}]{\pi }}\,{\Gamma {\bigl (}{\tfrac {3}{4}}{\bigr )}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29817a4531027f1991bbfc9b6088ad7d69dfe80c)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\vartheta _{00}{\bigl \{}q{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}{\bigr \}}={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}}=2^{-1/6}3^{-1/8}\pi ^{-1/2}\beta ({\tfrac {1}{3}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa46c0d5937150c2e68e08feb6c74fc90ba57244)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {2}}\,\pi )]=\vartheta _{00}[q({\sqrt {2}}-1)]={\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/8}\cos({\tfrac {1}{8}}\pi )\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4543eb5393ffa9c781b082c16a31d365f3e7d7bc)
![{\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=\vartheta _{01}[q({\sqrt {2}}-1)]={\sqrt[{4}]{2{\sqrt {2}}-2}}\,{\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/4}\cos({\tfrac {1}{8}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be0f87132d7e16c19584081deb88ecf76ea28e0d)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}={\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b5806ac256d4f9cbee2e600b107b796149525d2)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}=2^{1/4}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275164859145587e57e6dcec09ff6a14acdb50a5)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e434be718ca9f45eab55f4be6dbc809f452b143e)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/4}{\sqrt {{\sqrt {2}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/811f3b7a90a5c68d52be4b97dc0baa54896b6b34)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274ab98328bf81360ae485dd6c4ec3876c0b1677)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{-3/8}{\sqrt {{\sqrt {3}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e503d680361cd99abd6c5f17e2484532ec5c7cf)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9da6f4b51282acd6cdbb1f4f000e147120becd7)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}({\sqrt[{4}]{2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7e896b6a925a2e195d345679b8775787f9b92a2)

![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}5^{-1/2}({\sqrt[{4}]{5}}-1)^{2}\Phi ^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8941a32268dba27298e7fab0251b49ef306927f0)
![{\displaystyle {\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62eae1843959ef981d29f3c7b929bd157cdaa3f5)
![{\displaystyle \vartheta _{00}({\text{e}}^{-6\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb035a3d45e2ab6f147fe0bec8d206162c2a15a0)
![{\displaystyle \vartheta _{00}({\text{e}}^{-7\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/079109c07c2dd02b4822f57cae3d61bb0d7cf3cf)
![{\displaystyle \vartheta _{00}({\text{e}}^{-8\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}({\sqrt {2+{\sqrt {2}}}}+2^{7/8})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc00f43c5679fce7a316e3bdef61c4d133592207)
![{\displaystyle \vartheta _{00}({\text{e}}^{-9\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f877403163382ad95f8da98d21b4d2fc205092)
![{\displaystyle \vartheta _{00}({\text{e}}^{-10\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}5^{-1/2}\Phi ^{3/2}\cos {\bigl [}{\tfrac {1}{4}}\arcsin {\bigl (}\Phi ^{-12}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0756934d88de0d3a5d8008ead1b12d77476f501d)
![{\displaystyle \vartheta _{00}({\text{e}}^{-11\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/4}11^{-5/8}{\sqrt {{\sqrt {11}}+3}}\,{\bigl \{}4+{\sqrt {11}}-3{\sqrt {3}}\tanh {\bigl [}{\tfrac {1}{4}}\operatorname {arcosh} ({\tfrac {7}{4}})+{\tfrac {1}{2}}\operatorname {artanh} ({\tfrac {4}{9}}{\sqrt {3}})-{\tfrac {1}{6}}\operatorname {artanh} ({\tfrac {1}{27}}{\sqrt {3}}){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb81295f05f9079f715931c7109b1d0979be3d)
![{\displaystyle \vartheta _{00}({\text{e}}^{-12\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-2}3^{-3/8}{\sqrt {\cot({\tfrac {1}{24}}\pi )}}({\sqrt[{4}]{3}}+1)({\sqrt {3}}+1-{\sqrt[{4}]{12}})\cos {\bigl \{}{\tfrac {1}{2}}\arcsin {\bigl [}{\tfrac {1}{2}}(2+{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})^{2}({\sqrt {2}}-1)^{2}({\sqrt[{4}]{3}}-1)^{4}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3535d0f5aff637d7fa1f5fb731bda1ca56232042)
![{\displaystyle \vartheta _{00}({\text{e}}^{-13\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}13^{-1/2}{\sqrt {5{\sqrt {13}}+18}}\,{\bigl \{}{\tfrac {1}{6}}(5{\sqrt {39}}-17{\sqrt {3}})\coth {\bigl [}{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {6}{11}}{\sqrt {3}})-{\tfrac {1}{2}}\operatorname {arcosh} {\bigl (}{\tfrac {4}{13}}{\sqrt {13}}{\bigr )}{\bigr ]}-{\tfrac {1}{2}}({\sqrt {13}}-3){\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbc8bbd8eb051776538f7399d9241cc7bad6994)
![{\displaystyle \vartheta _{00}({\text{e}}^{-14\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-5/8}7^{-7/16}{\sqrt[{4}]{3+{\sqrt {7}}}}{\sqrt {5-{\sqrt {7}}+{\sqrt[{4}]{28}}}}\,\cos {\bigl \{}{\tfrac {1}{4}}\arcsin {\bigl [}({\tfrac {1}{4}}{\sqrt {14}}+{\tfrac {1}{4}}{\sqrt {2}}-{\tfrac {1}{2}}{\sqrt[{4}]{7}})^{12}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de4c6ae2063c452fd09f57285b304c98b262873a)
![{\displaystyle \vartheta _{00}({\text{e}}^{-15\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1/2}5^{-1/2}\Phi ^{3/2}{\bigl (}{\sqrt {2{\sqrt {1+\Phi ^{-8}+\Phi ^{-16}}}+2+\Phi ^{-8}}}+{\sqrt {1-\Phi ^{-8}}}{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e8482d7ff471533dd3dd6c13b6e1350a97e1c79)
![{\displaystyle \vartheta _{00}({\text{e}}^{-16\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}{\bigl [}2^{-9/4}({\sqrt[{4}]{2}}+1)+2^{-23/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c9e004698837d0e5da1653e6e8a2bd3ffd907e9)
![{\displaystyle \vartheta _{00}({\text{e}}^{-17\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-3/2}17^{-1/2}{\bigl [}({\sqrt[{4}]{17}}+1){\sqrt {{\sqrt {17}}-1}}+{\sqrt[{8}]{272}}{\sqrt {{\sqrt {17}}+3}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd0fe0c9e9a2064182136c689f2c5fe7d7e3a89)
![{\displaystyle \vartheta _{00}({\text{e}}^{-18\pi })={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}3^{-1}({\sqrt[{3}]{2{\sqrt {3}}+2}}+1)\cos {\bigl \langle }{\tfrac {1}{4}}\arcsin {\bigl \{}{\bigl [}2{\sqrt {3}}-3-{\sqrt {6}}(2-{\sqrt {3}})^{5/6}+{\sqrt {2}}(2-{\sqrt {3}})^{7/6}{\bigr ]}^{4}{\bigr \}}{\bigr \rangle }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/833c183d94b8f58204f266fe5054cf8ebf71adef)

![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{2}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}{\sqrt {{\sqrt {2}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6aef9793232d82700431269f0815b5196af0e44)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{3}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}2^{-1/4}3^{1/8}{\sqrt {{\sqrt {3}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee33b151e0a465dae4144dcc937f2f7ab5227cd)
![{\displaystyle \vartheta _{00}[\exp(-\pi /y)]={\sqrt {y}}\,\vartheta _{00}[\exp(-\pi y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae9008aff5514d5f893a3af0c31690ed0e2840dd)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{5}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efd9be14fcf890ef00e931f62fdf1a515456e2a7)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{7}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07276f2086d328e6cd6834054e515b6182a8e66b)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{9}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1b32c080a70e149757e8a2beaff03fef283b7b4)
![{\displaystyle \vartheta _{00}[\exp(-{\tfrac {1}{11}}\pi )]={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46dcf55254335c5b6c089421248fb9c16cccebd0)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}=2^{1/3}3^{1/8}{\sqrt {\omega _{2}/\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6d5f8eb824d43ce521b68d94407b70feb8896fa)
![{\displaystyle \vartheta _{00}[\exp(-2{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}\cos({\tfrac {1}{24}}\pi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ff9967dce3b0989b6ab4ae153b98767a3a08c5)
![{\displaystyle \vartheta _{00}[\exp(-3{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-7/8}\beta ({\tfrac {1}{3}})^{1/2}({\sqrt[{3}]{2}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e1b28ec514bb28b4a21769d27dc53eda142872d)
![{\displaystyle \vartheta _{00}[\exp(-4{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-7/6}3^{-1/8}\beta ({\tfrac {1}{3}})^{1/2}[1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d1a15726742041d3cbd480d532593d3a4d4516)
![{\displaystyle \vartheta _{00}[\exp(-5{\sqrt {3}}\,\pi )]=\pi ^{-1/2}2^{-1/6}3^{-9/8}\beta ({\tfrac {1}{3}})^{1/2}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f741bdad21e8b749424137653d6029be72b216)

![{\displaystyle \vartheta _{01}[\exp(-{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aff2b55af25b0f4add279d206e80df5b5c13ab5)
![{\displaystyle \vartheta _{01}[\exp(-3{\sqrt {2}}\,\pi )]=2^{-1/4}3^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {{\sqrt {3}}+{\sqrt {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1540d7a0e53edd834ffa54f957a95bbb558d41ec)
![{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{3}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {{\sqrt {3}}-{\sqrt {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a44b17586927df382f85aca4b9cb0f055ccdbd6)
![{\displaystyle \vartheta _{01}[\exp(-5{\sqrt {2}}\,\pi )]=2^{-1/4}5^{-1/2}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {2{\text{g}}(50)+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2690db0f9bf83eaecd5375715f998f9055f95f9)
![{\displaystyle \vartheta _{01}[\exp(-{\tfrac {1}{5}}{\sqrt {2}}\,\pi )]=2^{-1/4}\pi ^{-1/2}{\sqrt {\cos({\tfrac {1}{8}}\pi )\beta ({\tfrac {3}{8}})}}{\sqrt {1-2{\text{g}}(50)^{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0e67e8b9399deb1e5f5afe2e5aae101327e87ad)

![{\displaystyle {\text{g}}(50)=w_{R5}({\sqrt {2}}-1)=2\,[\exp(-5\,{\sqrt {2}}\,\pi );\exp(-10\,{\sqrt {2}}\,\pi )]_{\infty }[\exp(-{\sqrt {2}}\,\pi );\exp(-2\,{\sqrt {2}}\,\pi )]_{\infty }^{-5}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087548aa1f1d90d6bd606a0bba3561e6c6133fc6)
![{\displaystyle ={\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}^{2}-{\tfrac {1}{2}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dc52ba4cd236ac785d66d8724571040ca142582)
![{\displaystyle ={\bigl \langle }{\tfrac {1}{2}}-{\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}^{2}{\bigr \rangle }^{-1}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1200af9f737060de043135a2523e11846dfdf722)
![{\displaystyle =\Phi ^{-1}\cot {\bigl [}{\tfrac {1}{4}}\pi -\arctan {\bigl (}{\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}{\bigr )}{\bigr ]}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02afa7c62833bdba3eb12f04530c1f633cb381e3)





![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {5}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl \{}\sin {\bigl [}{\tfrac {1}{2}}\arcsin({\sqrt {5}}-2){\bigr ]}{\bigr \}}}}=2^{-17/40}5^{-5/16}({\sqrt {5}}+1)^{5/8}\cos({\tfrac {1}{20}}\pi )^{1/2}\pi ^{-1/2}{\sqrt {\beta ({\tfrac {9}{20}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50b45c2912b6b1f6e5d84a40f47f646d45ecb87f)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {7}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{8}}(3{\sqrt {2}}-{\sqrt {14}}){\bigr ]}}}=2^{-2/7}7^{-5/8}\cot({\tfrac {1}{7}}\pi )^{1/2}\,\pi ^{-1}{\sqrt {\beta ({\tfrac {2}{7}})\beta ({\tfrac {4}{7}})\beta ({\tfrac {5}{14}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e175eb28ef699006c9d75753adad0c94c6af56ce)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {15}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{16}}({\sqrt {10}}-{\sqrt {6}})(3-{\sqrt {5}})(2-{\sqrt {3}}){\bigr ]}}}=2^{-3/2}3^{-5/8}5^{-5/8}({\sqrt {5}}+1)\,\pi ^{-1}{\sqrt {\beta ({\tfrac {2}{15}})\beta ({\tfrac {8}{15}})\beta ({\tfrac {1}{3}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc7379f36eb4c95d3df23e5dfacd4dc5d2913280)
![{\displaystyle \vartheta _{00}[\exp(-{\sqrt {11}}\,\pi )]={\sqrt {2\pi ^{-1}K{\bigl \{}\sin {\bigl [}{\tfrac {1}{2}}\arcsin({\tfrac {1}{2}}T_{TRI}^{-4}){\bigr ]}{\bigr \}}}}={2}^{9/22}{11}^{-3/8}{\pi }^{-1/2}(T_{TRI}^{2}-{T_{TRI}}){\sqrt {\cos({\tfrac {1}{22}}\pi )\cos({\tfrac {3}{22}}\pi )\mathrm {B} ({\tfrac {5}{22}};{\tfrac {15}{22}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbb90867f22f2833b7ef702d28791e97513d6d61)
![{\displaystyle T_{TRI}={\tfrac {1}{3}}{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\tfrac {1}{3}}={\tfrac {1}{2}}{\bigl (}{\tfrac {2}{3}}+{\tfrac {1}{3}}{\sqrt[{3}]{3{\sqrt {33}}+17}}-{\tfrac {1}{3}}{\sqrt[{3}]{3{\sqrt {33}}-17}}{\bigr )}^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9173a3fc1a4ebd774ad9910a25580e2c60b36a70)




![{\displaystyle \vartheta '_{00}(x)=\vartheta _{00}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{01}(x)^{2}}{4x}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5085246c161248a3259cb1c6a9b388f14ade63e6)
![{\displaystyle \vartheta '_{00}({\text{e}}^{-\pi })={\frac {{\text{e}}^{\pi }{\sqrt {G}}}{2{\sqrt[{4}]{8}}\,\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c0da746ce7ef84ae27a645b24c1caf2e91f20d3)
![{\displaystyle \vartheta '_{00}({\text{e}}^{-\pi /2})={\frac {\cos({\tfrac {1}{8}}\pi ){\text{e}}^{\pi /2}{\sqrt {G}}[({\sqrt {2}}-1)\pi G^{2}+1]}{{\sqrt[{4}]{2}}\,\pi }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77d818e4f809228587b86c2a9891156b528e5924)
![{\displaystyle \vartheta _{10}(x^{2})={\tfrac {1}{2}}{\sqrt {2[\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc9bd97eafef2da346b986c44278e04f423d95bd)
![{\displaystyle \vartheta _{00}(x^{2})={\tfrac {1}{2}}{\sqrt {2[\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5a54d7761b6db328cc78be2dee8bc20a83184e8)


![{\displaystyle 27\,\vartheta _{00}(x^{3})^{8}-18\,\vartheta _{00}(x^{3})^{4}\vartheta _{00}(x)^{4}-\,\vartheta _{00}(x)^{8}=8\,\vartheta _{00}(x^{3})^{2}\vartheta _{00}(x)^{2}[2\,\vartheta _{01}(x)^{4}-\vartheta _{00}(x)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe6c0b4ed1a7010a802637bbbc211ffb24e3526)
![{\displaystyle 27\,\vartheta _{01}(x^{3})^{8}-18\,\vartheta _{01}(x^{3})^{4}\vartheta _{01}(x)^{4}-\,\vartheta _{01}(x)^{8}=8\,\vartheta _{01}(x^{3})^{2}\vartheta _{01}(x)^{2}[2\,\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d981666970f7bc4250a2030d31e4ffac5b96608)
![{\displaystyle [\vartheta _{00}(x)^{2}-\vartheta _{00}(x^{5})^{2}][5\,\vartheta _{00}(x^{5})^{2}-\vartheta _{00}(x)^{2}]^{5}=256\,\vartheta _{00}(x^{5})^{2}\vartheta _{00}(x)^{2}\vartheta _{01}(x)^{4}[\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34d31f83d29921403d740556f198dc1e222c079a)
![{\displaystyle [\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}][5\,\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}]^{5}=256\,\vartheta _{01}(x^{5})^{2}\vartheta _{01}(x)^{2}\vartheta _{00}(x)^{4}[\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fe7af92061688ce1c235885e4fc5c57ca2625b4)
![{\displaystyle {\biggl [}{\frac {\vartheta _{00}(x^{1/3})^{2}}{\vartheta _{00}(x)^{2}}}-{\frac {3\,\vartheta _{00}(x^{3})^{2}}{\vartheta _{00}(x)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\vartheta _{10}(x)^{2}\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{4}}}{\biggr ]}^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3e9e97311736c32ad24533b1730a6556e4d20)
![{\displaystyle {\biggl [}{\frac {3\,\vartheta _{01}(x^{3})^{2}}{\vartheta _{01}(x)^{2}}}-{\frac {\vartheta _{01}(x^{1/3})^{2}}{\vartheta _{01}(x)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\vartheta _{10}(x)^{2}\vartheta _{00}(x)^{2}}{\vartheta _{01}(x)^{4}}}{\biggr ]}^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42623c1f5ba6b7c0b4bd68e80a41d51487a7489f)
![{\displaystyle R(x)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b757250844d30ae1365b456dc76dededbef3a3b7)
![{\displaystyle R(x^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\vartheta _{01}(x)^{2}}{2\vartheta _{01}(x^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed4b62974c3e6df1186bfa9cebf7b9eaf742f1b5)
![{\displaystyle R(x^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7697c85e36fc8e963889d7074804ce1c3bfbe389)
![{\displaystyle S(x)={\frac {R(x^{4})}{R(x^{2})R(x)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\vartheta _{00}(x)^{2}}{2\vartheta _{00}(x^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52ebedd8d928263bc4ec2e8721d16102fbe8d95b)
![{\displaystyle {\frac {\vartheta _{00}(x^{1/5})}{\vartheta _{00}(x^{5})}}-1={\frac {1}{S(x)}}[S(x)^{2}+R(x^{2})][1+R(x^{2})S(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2a1e2e5a0baaa7011cee52c12c8ea8d2aebd43d)
![{\displaystyle 1-{\frac {\vartheta _{01}(x^{1/5})}{\vartheta _{01}(x^{5})}}={\frac {1}{R(x)}}[R(x^{2})+R(x)^{2}][1-R(x^{2})R(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b44859a2d16d142b0c33f92522bf400fb15d548)



![{\displaystyle {\biggl [}{\frac {\vartheta _{00}(x^{1/5})^{2}}{\vartheta _{00}(x)^{2}}}-1{\biggr ]}{\biggl [}{\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{01}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{01}(x)}}+1{\biggr ]}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27b53df22018d972e84ea9a57b4220c6fd6147f7)
![{\displaystyle {\biggl [}1-{\frac {\vartheta _{01}(x^{1/5})^{2}}{\vartheta _{01}(x)^{2}}}{\biggr ]}{\biggl [}{\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{00}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{00}(x)}}-1{\biggr ]}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57bfcddf1d69cc2b80daa1d7714d7868f5fe2e9d)
![{\displaystyle {\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{01}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{01}(x)}}+1={\frac {4\,\vartheta _{00}(x^{5})^{2}}{5\,\vartheta _{00}(x^{5})^{2}-\vartheta _{00}(x)^{2}}}{\biggl [}-1+{\frac {S(x)}{R(x^{2})}}+{\frac {R(x^{2})}{S(x)}}+{\frac {1}{R(x^{2})}}-{\frac {1}{S(x)^{2}}}-R(x^{2})-S(x)^{2}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99757b49625c4470e6c796a85e798cec3d288808)
![{\displaystyle {\frac {\vartheta _{10}(x^{1/5})\,\vartheta _{00}(x^{1/5})}{\vartheta _{10}(x)\,\vartheta _{00}(x)}}-1={\frac {4\,\vartheta _{01}(x^{5})^{2}}{5\,\vartheta _{01}(x^{5})^{2}-\vartheta _{01}(x)^{2}}}{\biggl [}1+{\frac {R(x)}{R(x^{2})}}+{\frac {R(x^{2})}{R(x)}}-{\frac {1}{R(x^{2})}}+{\frac {1}{R(x)^{2}}}+R(x^{2})+R(x)^{2}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e49e562e803a4f3f9a8096b659441ab5a5d3c01)
![{\displaystyle \vartheta _{01}[q(k)]=\vartheta _{01}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/142d9b6c0318fd8aa46dd5b0f55f8f1f12d89db4)
![{\displaystyle \vartheta _{01}[q(k)^{2}]=\vartheta _{00}[q(k)]{\sqrt[{8}]{1-k^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34d5533e7c3b48252b469dc16aa1891622070b17)
![{\displaystyle \vartheta _{00}[q(k)^{2}]=\vartheta _{00}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55819ea1141443ce9aabc28d3779779189fe47f4)
![{\displaystyle \vartheta _{00}[q(k)^{3}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{3}}K(k);k]}{{\sqrt {3}}\,{\text{cd}}[{\tfrac {2}{3}}K(k);k]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b01d5e5e1322fd9c883d1e285fb0537938111a9)
![{\displaystyle \vartheta _{00}[q(k)^{5}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{5}}K(k);k]\,{\text{sn}}[{\tfrac {4}{5}}K(k);k]}{{\sqrt {5}}\,{\text{cd}}[{\tfrac {2}{5}}K(k);k]\,{\text{cd}}[{\tfrac {4}{5}}K(k);k]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebd9595c5d1784b5fb786f0089082d0a83c7b0f9)
![{\displaystyle \vartheta _{00}[q(k)^{7}]=\vartheta _{00}[q(k)]\,{\frac {{\text{sn}}[{\tfrac {2}{7}}K(k);k]\,{\text{sn}}[{\tfrac {4}{7}}K(k);k]\,{\text{sn}}[{\tfrac {6}{7}}K(k);k]}{{\sqrt {7}}\,{\text{cd}}[{\tfrac {2}{7}}K(k);k]\,{\text{cd}}[{\tfrac {4}{7}}K(k);k]\,{\text{cd}}[{\tfrac {6}{7}}K(k);k]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4352b3d467e08856362143684848a6ac3291dc85)
![{\displaystyle \vartheta _{01}{\bigl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}^{3}{\bigr \rangle }=\vartheta _{01}{\bigl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}{\bigr \rangle }\,3^{-1/2}\,{\bigl (}{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/651f05af9cf210233a7b47f882ce2f4c60719720)
![{\displaystyle \vartheta _{01}{\bigl [}q(\varepsilon )^{5}{\bigr ]}=\vartheta _{01}{\bigl [}q(\varepsilon ){\bigr ]}5^{-1/2}{\sqrt {2\,w_{R5}(\varepsilon )+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2eed57e0f7a35b55ab1fb6dedd47754d5fb3bd4)
![{\displaystyle \vartheta _{00}{\bigl [}q(\varepsilon )^{5}{\bigr ]}=\vartheta _{00}{\bigl [}q(\varepsilon ){\bigr ]}5^{-1/2}{\sqrt {2\,W_{R5}(\varepsilon )+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b46b3423d753dd05e18ae66c013e03c3cac9d78a)

![{\displaystyle w_{R5}(\varepsilon )={\frac {2\,[q(\varepsilon )^{5};q(\varepsilon )^{10}]_{\infty }}{[q(\varepsilon );q(\varepsilon )^{2}]_{\infty }^{5}}}={\text{nc}}{\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}-{\text{nc}}{\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac14ff91ae1a41ac70970ca6a75e0ac04805709)
![{\displaystyle w_{R5}(\varepsilon )^{6}-2\,w_{R5}(\varepsilon )^{5}=\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigl [}2\,w_{R5}(\varepsilon )+1{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9bebee3d1da6505ad586364e2171972eff42387)

![{\displaystyle W_{R5}(\varepsilon )=2\,w_{R5}(\varepsilon )^{-1}\,w_{R5}[\varepsilon ^{2}(1+{\sqrt {1-\varepsilon ^{2}}})^{-2}]={\text{dn}}{\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}+{\text{dn}}{\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a9c40a2a4af3d5a668a51501e95b241fd4b024d)
![{\displaystyle 2\,W_{R5}(\varepsilon )^{5}-W_{R5}(\varepsilon )^{6}=\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigl [}2\,W_{R5}(\varepsilon )+1{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d719ac5e4554f43c5292827ea4060a93e39e3e04)

![{\displaystyle q{\bigl \langle }\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}({\color {blueviolet}{\tfrac {3}{2}}-{\tfrac {1}{2}}{\sqrt {5}}})^{3}{\bigr ]}{\bigr \}}{\bigr \rangle }={\color {blue}\exp(-{\sqrt {10}}\,\pi )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be65983aad66f296cff1bea46b3b87e54be7a85)
![{\displaystyle {\color {ForestGreen}\vartheta _{01}[{\color {Navy}\exp(-3{\sqrt {10}}\,\pi )}]=\vartheta _{01}[{\color {blue}\exp(-{\sqrt {10}}\,\pi )}]\,6^{-1/2}\,{\bigl [}(3-{\sqrt {5}}){\sqrt {({\sqrt {6}}+{\sqrt {5}})(3+{\sqrt {6}})}}+{\sqrt {15}}-{\sqrt {3}}{\bigr ]}^{1/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c29e2328c8fd2381b5d21eaaded7fbc51124297)

![{\displaystyle q{\bigl \langle }\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\bigl (}{\color {blueviolet}{\sqrt {2}}+{\tfrac {1}{2}}-{\tfrac {1}{2}}{\sqrt {4{\sqrt {2}}+5}}}{\bigr )}^{3}{\bigr ]}{\bigr \}}{\bigr \rangle }={\color {blue}\exp(-{\sqrt {14}}\,\pi )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d507daf5f0239ad8b3a386a6cde578519a9870a9)
![{\displaystyle {\color {ForestGreen}\vartheta _{01}[{\color {Navy}\exp(-3{\sqrt {14}}\,\pi )}]=\vartheta _{01}[{\color {blue}\exp(-{\sqrt {14}}\,\pi )}]\,6^{-1/2}\,{\bigl (}{\sqrt {12{\sqrt {2}}+15}}+{\sqrt {8{\sqrt {2}}+11}}-{\sqrt {7}}-{\sqrt {3}}{\bigr )}^{1/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2d1a59d27ab266310535dfb365a4d5ae5e1cf6)


![{\displaystyle \vartheta _{00}(x;c^{1/2})=[\vartheta _{00}(c)^{2}+\vartheta _{10}(c)^{2}]^{-1/2}[\vartheta _{00}(x;c)^{2}+\vartheta _{10}(x;c)^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de3906cde7f004fc1c3ec28b825bc85c8ddd8241)
![{\displaystyle \vartheta _{01}(x;c^{1/2})=[\vartheta _{00}(c)^{2}-\vartheta _{10}(c)^{2}]^{-1/2}[\vartheta _{00}(x;c)^{2}-\vartheta _{10}(x;c)^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38ce7823276a4c32839dc429ce2a48b45417ecbf)

![{\displaystyle \vartheta _{00}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})[1+2\cos(x)c^{2n-1}+c^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52a508981f0daeeaf63637846c14b2173a7f0081)
![{\displaystyle \vartheta _{01}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})[1-2\cos(x)c^{2n-1}+c^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dcfb023551b4d2630479e47a4aeeb3589c5ed41)
![{\displaystyle \vartheta _{00}({\tfrac {1}{2}}x;c)\,\vartheta _{00}({\tfrac {1}{2}}x;c)=\prod _{n=1}^{\infty }(1-c^{2n})^{2}[1+2\cos(x)c^{2n-1}+c^{4n-2}][1-2\cos(x)c^{2n-1}+c^{4n-2}]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94d37ad01a85b357ce414f3ada6f839b7f153801)
![{\displaystyle =\prod _{n=1}^{\infty }(1-c^{2n})^{2}\{1-2[2\cos(x)^{2}-1]c^{4n-2}+c^{8n-4}\}=\prod _{n=1}^{\infty }(1-c^{2n})^{2}[1-2\cos(2x)c^{4n-2}+c^{8n-4}]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/531a185282c271d18efda8d9af343735076e0aa0)
![{\displaystyle ={\biggl [}\prod _{n=1}^{\infty }{\frac {1-c^{2n}}{1+c^{2n}}}{\biggr ]}{\biggl \{}\prod _{n=1}^{\infty }(1-c^{4n}){\bigl [}1-2\cos(2x)c^{4n-2}+c^{8n-4}{\bigr ]}{\biggr \}}={\biggl [}\prod _{n=1}^{\infty }{\frac {1-c^{2n}}{1+c^{2n}}}{\biggr ]}\vartheta _{01}(x,c^{2})=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9816af0890e335ffc7dee0307d05bae47736b8a8)

![{\displaystyle q(k)=\exp[-\pi K({\sqrt {1-k^{2}}})K(k)^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/943ebbf1e09e3324c38f46c396be2ce658e327fc)

![{\displaystyle \vartheta _{00}[0;q(k)]={\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d6c2cb05bf0e49ee8d256021fd242dc63dad99)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{2}}\pi ;q(k)]={\sqrt[{4}]{1-k^{2}}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0deef1e32f5a6ee77b954a10e9ea173b117a52c7)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{4}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{8}}{\sqrt[{16}]{1-k^{2}}}{\sqrt[{4}]{1+{\sqrt {1-k^{2}}}}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03f9b57f8c387e01d0e840c877ca982195e66a70)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{6}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{12}]{1-k^{2}}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {1}{3}}K(k);k]\operatorname {nc} [{\tfrac {2}{3}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab107bba0ee92f59784203b9b7adfb4d73b545a)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{3}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {2}{3}}K(k);k]\operatorname {dc} [{\tfrac {2}{3}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8425171fd99fbc7a8417650de4c1b2442961cc97)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{10}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {nd} [{\tfrac {4}{5}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/551d3dae3c116874af9476485905bf1c2057a044)
![{\displaystyle \vartheta _{00}[{\tfrac {1}{5}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {dn} [{\tfrac {2}{5}}K(k);k]^{4}}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e394b9d9de17ae69a4ca8dd11d9f996b3fcd5e0)
![{\displaystyle \vartheta _{00}[{\tfrac {3}{10}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {nd} [{\tfrac {2}{5}}K(k);k]}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f49db29894d4ac900f11d97a1c0c9560c0cf5e2)
![{\displaystyle \vartheta _{00}[{\tfrac {2}{5}}\pi ;q(k)]={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {dn} [{\tfrac {4}{5}}K(k);k]^{4}}}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11c5f4404b168a6c9e95c05448dabe5d130d41eb)





![{\displaystyle \vartheta _{00}({\tfrac {1}{4}}\pi ;{\text{e}}^{-\pi })=2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1fd25ce80551a017653a550f40d3a38a26233f3)
![{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{6}]{2+{\sqrt {3}}}}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51c13fb375b2bc11b6402ec0de05b7abd383caa9)
![{\displaystyle \vartheta _{00}({\tfrac {1}{5}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{5}]{2({\sqrt {5}}+2)\cos({\tfrac {1}{20}}\pi )\tan({\tfrac {3}{20}}\pi )}}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ac76e7562a5438fe923a613023e0cf5ff718dd5)
![{\displaystyle \vartheta _{00}({\tfrac {2}{5}}\pi ;{\text{e}}^{-\pi })=2^{-1/4}{\sqrt[{5}]{2({\sqrt {5}}+2)\sin({\tfrac {1}{20}}\pi )\cot({\tfrac {3}{20}}\pi )}}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93df0f9628ed2db4c4db38636100d97e691b725c)


![{\displaystyle \vartheta _{00}({\tfrac {1}{2}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-5/8}{\sqrt[{4}]{{\sqrt {2}}+1}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c3de06f6337f3fbe46889b38b4f3a03f0c755e)
![{\displaystyle \vartheta _{00}({\tfrac {1}{6}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-9/8}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt[{3}]{{\sqrt {3}}+{\sqrt {2}}}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/245476bd0be94ba90ad131a15e3f9af34d7a5fe7)
![{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-{\sqrt {2}}\pi })=2^{-1/8}\sin({\tfrac {5}{24}}\pi ){\sqrt[{3}]{{\sqrt {3}}+{\sqrt {2}}}}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ff67f100d485fcbed507112b017f39f76314922)
![{\displaystyle k=\lambda ^{*}(5)=\sin[{\tfrac {1}{2}}\arcsin({\sqrt {5}}-2)]\colon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4e07c04e5a3e3021a63612d5375ffe8d209205)

![{\displaystyle \vartheta _{00}({\tfrac {1}{6}}\pi ;{\text{e}}^{-{\sqrt {5}}\pi })=2^{-47/40}5^{-5/16}({\sqrt {2{\sqrt {5}}-2{\sqrt {3}}+1}}+1){\sqrt[{8}]{{\sqrt {5}}-1}}{\sqrt[{6}]{4+{\sqrt {15}}}}\cos({\tfrac {1}{20}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {9}{20}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1ffb53d69b7b8672206e2a7d216bcfccb01542c)
![{\displaystyle \vartheta _{00}({\tfrac {1}{3}}\pi ;{\text{e}}^{-{\sqrt {5}}\pi })=2^{-37/40}5^{-5/16}({\sqrt {5}}+1)^{5/8}{\sqrt[{6}]{4+{\sqrt {15}}}}\cos({\tfrac {1}{20}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {9}{20}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe12ef80183629d4631bb0c79dc6b26a028de9df)



![{\displaystyle \vartheta _{01}'(v;w)={\frac {\partial }{\partial v}}\vartheta _{01}(v;w)={\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]}\vartheta _{01}(v;w)\,{\text{zn}}{\biggl \{}{\frac {v}{2}}{\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]};{\frac {\vartheta _{00}(w)^{2}-\vartheta _{01}(w)^{2}}{\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}}}{\biggr \}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e24564e4d453a95765ccd6fdfc40a51a1165ea5)

![{\displaystyle \vartheta _{00}'(v;w)={\frac {\partial }{\partial v}}\vartheta _{00}(v;w)={\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]}\vartheta _{00}(v;w)\,{\text{zn}}{\biggl \{}{\frac {v}{2}}{\bigl [}\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}{\bigr ]};{\frac {\vartheta _{00}(w)^{2}-\vartheta _{01}(w)^{2}}{\vartheta _{00}(w)^{2}+\vartheta _{01}(w)^{2}}}{\biggr \}}-}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d9e995e2c9e1b010d798a71a2fdbe9d7612608)

![{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{01}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{01}[x;q(k)]{\text{zn}}[2\pi ^{-1}K(k)x;k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79fa25acbc9aa223b33caf54e19dd20ee6a11f6e)
![{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{00}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{00}[x;q(k)]\{{\text{zn}}[2\pi ^{-1}K(k)x;k]-k^{2}{\text{sn}}[2\pi ^{-1}K(k)x;k]{\text{cd}}[2\pi ^{-1}K(k)x;k]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7962ab453f4ce5e4903de050556c5f1f9343b2e9)
![{\displaystyle {\frac {\partial }{\partial x}}\vartheta _{10}[x;q(k)]=2\pi ^{-1}K(k)\vartheta _{10}[x;q(k)]\{{\text{zn}}[2\pi ^{-1}K(k)x;k]-{\text{sn}}[2\pi ^{-1}K(k)x;k]{\text{dc}}[2\pi ^{-1}K(k)x;k]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef3f4d401a1a7ab5ef7dcedd9f71ac56d4140aa)
![{\displaystyle {\text{zn}}(z;k)=E[{\text{am}}(z;k);k]-E(k)K(k)^{-1}z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa63569d87254031e94eca6a39a61c34b927ca8d)








![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{10}(x)={\frac {1}{2\pi x}}\vartheta _{10}(x)\vartheta _{00}(x)^{2}E{\biggl [}{\frac {\vartheta _{10}(x)^{2}}{\vartheta _{00}(x)^{2}}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e84cd43077be6186141b44bfcaa9c1575bafada2)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{00}(x)=\vartheta _{00}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{01}(x)^{2}}{4x}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf281c3f5561e384cc0481d485fde75ff3293f67)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{01}(x)=\vartheta _{01}(x){\bigl [}\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\vartheta _{00}(x)^{2}-\vartheta _{01}(x)^{2}}{\vartheta _{00}(x)^{2}+\vartheta _{01}(x)^{2}}}{\biggr ]}-{\frac {\vartheta _{00}(x)^{2}}{4x}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ebd20be5b0d91ff51a243c43e3ef95e8153e2aa)
![{\displaystyle \vartheta _{01}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{00}(x){\biggr ]}-\vartheta _{00}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{01}(x){\biggr ]}={\frac {1}{4x}}\,\vartheta _{00}(x)\,\vartheta _{01}(x){\bigl [}\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d532e3834f54a3b410649491f3178ab4d710560)






![{\displaystyle \int _{0}^{\infty }x^{n}\{\vartheta _{00}[\exp(-x)]-1\}\,\mathrm {d} x=2\Gamma (n+1)\zeta (2n+2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95510339a44713370caab4691ddbdfc27884d664)
![{\displaystyle \zeta (3)=\pi ^{-1/2}\int _{0}^{\infty }{\sqrt {x}}\,\{\vartheta _{00}[\exp(-x)]-1\}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de84f26cdd8c745042a8105a66dcb00724bbc3ad)
![{\displaystyle \gamma =\int _{0}^{\infty }{\frac {1}{2x}}[\exp(x^{2})\operatorname {erfc} (x)+2\pi ^{-1/2}x-1]\{\vartheta _{00}[\exp(-x^{2})]-1\}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d8e33ed833fcc10d98232fa9e6ee5a70009d81d)
![{\displaystyle \gamma =\sum _{n=1}^{\infty }{\biggl [}{\frac {\zeta (2n)}{2n}}-{\frac {\zeta (2n+1)}{2n+1}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad36557152cc3bb0e4729ab7eea849546c24a70b)
![{\displaystyle \int _{0}^{\infty }x^{n}\{\vartheta _{00}[\pi \,a;\exp(-x)]-1\}\,\mathrm {d} x=\Gamma (n+1)\zeta (2n+2)/\zeta (-2n-1){\bigl [}\zeta (-2n-1;a)+\zeta (-2n-1;1-a){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2faad6d77cca40d2e0679996faa0e2034eb0318)

![{\displaystyle {\bigl [}n\in \mathbb {C} \,\backslash {\bigl (}-{\tfrac {1}{2}}+m{\bigr )}(m\in \mathbb {N} ){\bigr ]}\cap {\bigl [}\mathrm {Re} (n)>-{\tfrac {1}{2}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80325efafdd8c8eefbc9328952402ea3f9691715)
![{\displaystyle \int _{0}^{\infty }{\sqrt[{4}]{x}}\{\vartheta _{00}[{\tfrac {1}{3}}\pi ;\exp(-x)]-1\}\,\mathrm {d} x=\Gamma ({\tfrac {5}{4}})\zeta ({\tfrac {5}{2}})/\zeta (-{\tfrac {3}{2}}){\bigl [}\zeta (-{\tfrac {3}{2}};{\tfrac {1}{3}})+\zeta (-{\tfrac {3}{2}};{\tfrac {2}{3}}){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68cc8d87582753e10906c43c0572bd301b887e01)
![{\displaystyle \zeta (y;z)={\frac {z^{1-y}}{y-1}}+{\frac {1}{2z^{y}}}+{\frac {2}{z^{y-1}}}\int \limits _{0}^{\infty }{\frac {\sin {\bigl [}y\arctan(x){\bigr ]}}{{(x^{2}+1)}^{y/2}{\bigl [}\exp(2\pi xz)-1{\bigr ]}}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b4d85d4575fda37467532111de5bf060d75798)

![{\displaystyle ={\frac {\sqrt {5}}{4}}\,\vartheta _{10}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{8}}{\bigl [}\vartheta _{00}(\Phi ^{-1})^{2}-\vartheta _{01}(\Phi ^{-1})^{2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c906dd29e77af17ce6f59a1fc787537c3343d4e)
![{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{24}}{\bigl [}2\vartheta _{10}(\Phi ^{-2})^{4}-\vartheta _{00}(\Phi ^{-2})^{4}+1{\bigr ]}={\frac {5}{24}}{\bigl [}\vartheta _{00}(\Phi ^{-2})^{4}-2\vartheta _{01}(\Phi ^{-2})^{4}+1{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/081afe6f5a8e85c66841ed1269b92c192b709528)
![{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{P_{2n-1}}}={\frac {1}{\sqrt {2}}}\,\vartheta _{10}{\bigl [}({\sqrt {2}}-1)^{2}{\bigr ]}^{2}={\frac {1}{2{\sqrt {2}}}}{\bigl [}\vartheta _{00}({\sqrt {2}}-1)^{2}-\vartheta _{01}({\sqrt {2}}-1)^{2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d871a2d6fdca3df549fc1d00d4a4070c595d5)
![{\displaystyle \sum _{k=-\infty }^{\infty }x^{ak^{2}+bk+c}=\exp {\bigl [}{\frac {4ac-b^{2}}{4a}}\ln(x){\bigr ]}{\bigl [}{\frac {-\pi }{a\ln(x)}}{\bigr ]}^{1/2}\vartheta _{00}{\bigl \{}{\frac {\pi b}{2a}};\exp {\bigl [}{\frac {\pi ^{2}}{a}}\ln(x)^{-1}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e559b587188b55187ca9b42d13b4ff6813a3956)
![{\displaystyle \sum _{k=-\infty }^{\infty }{\bigl (}{\frac {7}{11}}{\bigr )}^{5k^{2}+3k+2}={\bigl (}{\frac {7}{11}}{\bigr )}^{31/20}{\bigl (}{\frac {\pi }{5}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {11}{7}}{\bigr )}^{-1/2}\vartheta _{00}{\bigl \{}{\frac {3\pi }{10}};\exp {\bigl [}{\frac {1}{5}}\pi ^{2}\ln {\bigl (}{\frac {7}{11}}{\bigr )}^{-1}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52dde98bebae1dcaf7583e1b2ceea687ae65733c)
![{\displaystyle G(x,y,x',y')={\frac {1}{2\pi }}\operatorname {Re} \ln {\biggl \{}{\frac {\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy+x'-iy'),\exp(-\pi b/a)]\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy-x'+iy'),\exp(-\pi b/a)]}{\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy-x'-iy'),\exp(-\pi b/a)]\vartheta _{11}[{\tfrac {\pi }{2a}}(x+iy+x'+iy'),\exp(-\pi b/a)]}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae3b939e9d0230a37a52712cb84790672d580606)





![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}=q{\bigl \{}\mathrm {ctlh} {\bigl [}{\tfrac {1}{2}}\mathrm {aclh} (c){\bigr ]}^{2}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef828b03d1ec0e63b2eee4da412763786dc4f7b3)
![{\displaystyle x={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{4\,\vartheta _{10}(Q)\,\vartheta _{01}(Q)\,\vartheta _{00}(Q)}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29a2b379b710438381cbf89130488a8d6d801087)
![{\displaystyle ={\frac {{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}{\sqrt {\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5})}}}{2\,{\sqrt {2\,{\sqrt {c^{4}+1}}-2\,c^{2}}}\,\vartheta _{00}(Q)^{3}}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a584fbb450d3517458b0bf2821a6dd3ceea71b99)
![{\displaystyle ={\frac {256\,c\,\vartheta _{00}(Q)^{12}}{{\bigl (}{\sqrt {c^{4}+1}}+c^{2}{\bigr )}^{2}{\bigl [}\vartheta _{00}(Q^{1/5})^{2}-5\,\vartheta _{00}(Q^{5})^{2}{\bigr ]}^{4}{\bigl [}\vartheta _{00}(Q^{1/5})^{2}+5\,\vartheta _{00}(Q^{5})^{2}-4\,\vartheta _{00}(Q)^{2}-2\,\vartheta _{00}(Q^{1/5})\,\vartheta _{00}(Q^{5}){\bigr ]}^{2}+320\,\vartheta _{00}(Q)^{12}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c774f3fa1d24a29091c97b4c7857c7cf0dc241b)

![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c=1{\bigr )}=q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a0c37522775c49cdf66ecd87a5ae1814ae729c1)

![{\displaystyle x={\frac {\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}^{1/5}\}^{2}-5\,\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}^{5}\}^{2}}{4\,\vartheta _{10}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}\,\vartheta _{01}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}\,\vartheta _{00}\{q{\bigl [}{\frac {\sqrt[{4}]{2}}{2}}+\sin({\frac {\pi }{8}}){\bigr ]}\}}}\times }](https://wikimedia.org/api/rest_v1/media/math/render/svg/27325fca4eafb52c217a4b22aead1ab9c2904cb4)
![{\displaystyle \times {\sqrt {\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{1/5}\}^{2}+5\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{5}\}^{2}-4\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}\}^{2}-2\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{1/5}\}\,\vartheta _{00}\{q{\bigl [}{\tfrac {\sqrt[{4}]{2}}{2}}+\sin({\tfrac {\pi }{8}}){\bigr ]}^{5}\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2d46f674c8953f7305327bda2ecdcf44b320ce1)




![{\displaystyle Q=q{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}{\bigl (}c=2^{-3/4}{\bigr )}=q{\bigl [}\cos {\bigl (}{\tfrac {1}{8}}\pi {\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4065d42d8865ff1357d34612bddfcdb44ecda13)

![{\displaystyle x={\frac {\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}^{2}-5\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}^{2}}{{\sqrt {2}}\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}{\bigr \}}^{3}}}\times }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e899112a6309bebf9eec9840db522bab110dde96)
![{\displaystyle \times {\sqrt {\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}^{2}+5\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}^{2}-4\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}{\bigr \}}^{2}-2\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{1/5}{\bigr \}}\,\vartheta _{00}{\bigl \{}q{\bigl [}\cos({\tfrac {1}{8}}\pi ){\bigr ]}^{5}{\bigr \}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10299bf9c98b4e3065db8a43dfdaeaa9760ee467)

![{\displaystyle x={\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{50+75y-50y^{2}}}\cosh {\biggl \{}{\frac {1}{5}}\operatorname {arcosh} {\biggl [}{\frac {5{\sqrt {5+5y^{2}}}}{(1+2y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}-}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59339e1b69c79b11e8dc2f2ca499df60ed683156)
![{\displaystyle -{\frac {2}{5}}y^{-1/4}{\sqrt[{4}]{50+75y-50y^{2}}}\sinh {\biggl \{}{\frac {1}{5}}\operatorname {arsinh} {\biggl [}{\frac {5y{\sqrt {5+5y^{2}}}}{(2-y){\sqrt {4+6y-4y^{2}}}}}{\biggr ]}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7a4198f5ffb7409bcdf720219a51806a152370f)
![{\displaystyle y=W_{R5}{\bigl [}{\bigl (}2c^{2}+2+2{\sqrt {c^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {c^{4}+1}}+1}}+c{\bigr )}{\bigr ]}=W_{R5}{\bigl \{}\mathrm {ctlh} {\bigl [}{\tfrac {1}{2}}\mathrm {aclh} (c){\bigr ]}^{2}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c19aabc29307a2cc30a57afe1deb70602c95c593)

![{\displaystyle {\frac {1}{\pi }}=\sum _{n=0}^{\infty }{\frac {(4n)!\sin {\bigl \{}4\arctan {\bigl [}\varphi _{H}(x)^{4}{\bigr ]}{\bigr \}}^{2n}}{256^{n}(n!)^{4}}}\times }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6eca744f41cdc1a013263fc89da86c159733798c)
![{\displaystyle \times {\biggl \langle }{\frac {\pi ^{-1}\vartheta _{00}(x)^{-4}}{[1+\varphi _{H}(x)^{8}]}}-{\frac {\pi ^{-1}\ln(1/x)}{[1+\varphi _{H}(x)^{8}]^{2}}}{\biggl \{}{\frac {4x\vartheta '_{01}(x)[1+\varphi _{H}(x)^{8}]}{\vartheta _{01}(x)\vartheta _{00}(x)^{4}}}+2\varphi _{H}(x)^{8}{\biggr \}}+\pi ^{-1}\ln(1/x)\cos {\bigl \{}4\arctan {\bigl [}\varphi _{H}(x)^{4}{\bigr ]}{\bigr \}}n{\biggr \rangle }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d3ad4175d67545ae9111b763840392b405a1e46)











